题目内容
【题目】函数f(x)在[a,b]上有定义,若对任意x1 , x2∈[a,b],有 ![]() 则称f(x)在[a,b]上具有性质P.设f(x)在[1,3]上具有性质P,现给出如下命题:
则称f(x)在[a,b]上具有性质P.设f(x)在[1,3]上具有性质P,现给出如下命题:
①f(x)在[1,3]上的图象是连续不断的;
②f(x2)在[1, ![]() ]上具有性质P;
]上具有性质P;
③若f(x)在x=2处取得最大值1,则f(x)=1,x∈[1,3];
④对任意x1 , x2 , x3 , x4∈[1,3],有 ![]() [f(x1)+f(x2)+f(x3)+f(x4)]
[f(x1)+f(x2)+f(x3)+f(x4)]
其中真命题的序号是( )
A.①②
B.①③
C.②④
D.③④
【答案】D
【解析】解:在①中,反例:f(x)= 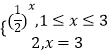 在[1,3]上满足性质P,
在[1,3]上满足性质P,
但f(x)在[1,3]上不是连续函数,故①不成立;
在②中,反例:f(x)=﹣x在[1,3]上满足性质P,但f(x2)=﹣x2在[1, ![]() ]上不满足性质P,
]上不满足性质P,
故②不成立;
在③中:在[1,3]上,f(2)=f( ![]() )≤
)≤ ![]() ,
,
∴ 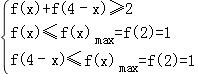 ,
,
故f(x)=1,
∴对任意的x1 , x2∈[1,3],f(x)=1,
故③成立;
在④中,对任意x1 , x2 , x3 , x4∈[1,3],
有 ![]() =
= ![]()
≤ ![]()
≤ ![]()
= ![]() [f(x1)+f(x2)+f(x3)+f(x4)],
[f(x1)+f(x2)+f(x3)+f(x4)],
∴ ![]() [f(x1)+f(x2)+f(x3)+f(x4)],
[f(x1)+f(x2)+f(x3)+f(x4)],
故④成立.
故选D.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

练习册系列答案
相关题目