题目内容
8.已知直线3x+4y-3=0与直线6x+my+14=0平行,则m的值是8.分析 利用直线平行的充要条件,求解即可.
解答 解:直线3x+4y-3=0与直线6x+my+14=0平行,
可得m=8,
故答案为:8.
点评 本题考查在的平行的条件的应用,基本知识的考查.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
19.点O是平行四边形ABCD的两条对角线的交点,则$\overrightarrow{AO}$+$\overrightarrow{OC}$+$\overrightarrow{CB}$等于( )
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{CD}$ | D. | $\overrightarrow{DA}$ |
3.函数y=sinx图象的对称轴方程可能是( )
| A. | x=-π | B. | x=$\frac{π}{4}$ | C. | x=π | D. | x=$\frac{3π}{2}$ |
13.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期的图象时,列表并填入的部分数据如下表:
(Ⅰ)求x1,x2,x3的值及函数f(x)的表达式;
(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,若直线y=k与函数y=f(x)g(x)的图象在[0,π]上有交点,求实数k的取值范围.
| x | $\frac{2π}{3}$ | x1 | $\frac{8π}{3}$ | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,若直线y=k与函数y=f(x)g(x)的图象在[0,π]上有交点,求实数k的取值范围.
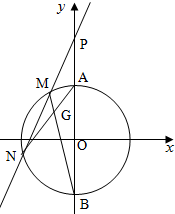 已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.
已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.