题目内容
设函数 的定义域为
的定义域为 ,若存在闭区间
,若存在闭区间 ,使得函数
,使得函数 满足:①
满足:① 在
在 上是单调函数;②
上是单调函数;② 在
在 上的值域是
上的值域是 ,则称区间
,则称区间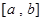 是函数
是函数 的“和谐区间”.下列结论错误的是( )
的“和谐区间”.下列结论错误的是( )
A.函数 ( ( )存在“和谐区间” )存在“和谐区间” |
B.函数 ( ( )不存在“和谐区间” )不存在“和谐区间” |
C.函数   )存在“和谐区间” )存在“和谐区间” |
D.函数 ( (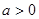 , ,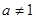 )不存在“和谐区间” )不存在“和谐区间” |
D
解析试题分析:根据“和谐区间”的定义,我们只要寻找到符合条件的区间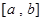 即可,对函数
即可,对函数 (
( ),“和谐区间”
),“和谐区间”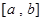
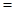
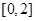 ,函数
,函数 是增函数,若存在“和谐区间”
是增函数,若存在“和谐区间” 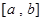 ,则
,则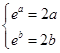 ,因此方程
,因此方程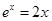 至少有两个不等实根,考虑函数
至少有两个不等实根,考虑函数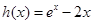 ,由
,由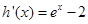
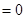 ,得
,得 ,可得
,可得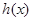 在
在 时取得最小值,而
时取得最小值,而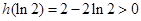 ,即
,即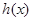 的最小值为正,
的最小值为正,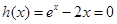 无实根,题设要求的
无实根,题设要求的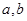 不存在,因此函数
不存在,因此函数 (
( )不存在“和谐区间”, 函数
)不存在“和谐区间”, 函数

 )的“和谐区间”为
)的“和谐区间”为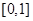 ,当然此时根据选择题的设置方法,知道应该选D,事实上,
,当然此时根据选择题的设置方法,知道应该选D,事实上, 在其定义域内是单调增函数,“和谐区间”
在其定义域内是单调增函数,“和谐区间”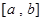 为
为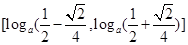 ,故D中的命题是错误的.
,故D中的命题是错误的.
考点:新定义的理解,函数的单调性,方程的解.

练习册系列答案
相关题目
函数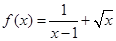 的定义域为( )
的定义域为( )
A.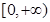 | B.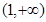 | C.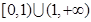 | D.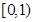 |
已知函数f(x)=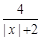 -1的定义域是[a,b](a,b∈Z),值域是[0,1],则满足条件的整数对(a,b)共有( )
-1的定义域是[a,b](a,b∈Z),值域是[0,1],则满足条件的整数对(a,b)共有( )
| A.2个 | B.5个 | C.6个 | D.无数个 |
设函数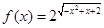 ,对于给定的正数
,对于给定的正数 ,定义函数
,定义函数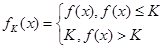 若对于函数
若对于函数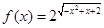 定义域内的任意
定义域内的任意 ,恒有
,恒有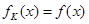 ,则( )
,则( )
A. 的最大值为 的最大值为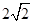 | B. 的最小值为 的最小值为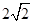 |
C. 的最大值为1 的最大值为1 | D. 的最小值为1 的最小值为1 |
己知函数f(x)= 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)- 有4个零点,则实数t的取值范围为( )
有4个零点,则实数t的取值范围为( )
A.(1, ) ) | B.( 1,-1) 1,-1) |
C.( 1,-1) 1,-1) (1, (1,  ) ) | D.( 1,-1) 1,-1) (1,2) (1,2) |
设方程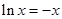 与方程
与方程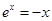 (其中e是自然对数的底数)的所有根之和为
(其中e是自然对数的底数)的所有根之和为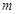 ,则( )
,则( )
A.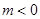 | B.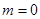 | C.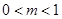 | D.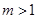 |
 的部分图像为( )
的部分图像为( )
 ,若方程
,若方程 有且只有两个不相等的实数根,则实数a的取值范围为 ( )
有且只有两个不相等的实数根,则实数a的取值范围为 ( ) B、
B、 C、
C、 D、
D、 。
。