题目内容
附加
 题:(本小题10分,实验班同学必做,其他班学生选做)
题:(本小题10分,实验班同学必做,其他班学生选做)是否存在常数a,使得函数f (x)=sin2x+acosx+
 -
-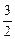 在闭区间
在闭区间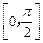 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.存在a=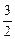 使得f (x)在闭区间
使得f (x)在闭区间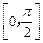 上的最大值为1
上的最大值为1
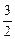 使得f (x)在闭区间
使得f (x)在闭区间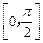 上的最大值为1
上的最大值为1解:f (x)=sin2x+acosx+ -
-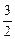
=1-cos2x+acosx+ -
-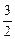 =-cos2x+acosx+
=-cos2x+acosx+ -
-
=-(cosx- a)2+
a)2+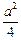 +
+ -
-
∵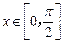 ,∴0≤cos
,∴0≤cos x≤1, ………………1分
x≤1, ………………1分
① 若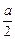 >1,即a>2,则当cosx=1时,f (x)取得最大值,
>1,即a>2,则当cosx=1时,f (x)取得最大值,
f (x)最大值=-(1- a)2+
a)2+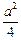 +
+ -
- =
=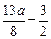 ……………3分
……………3分
令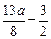 =1,解得
=1,解得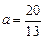 <2(舍去) ……………4分
<2(舍去) ……………4分
②若0≤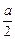 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=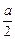 时,f (x)取得最大值,
时,f (x)取得最大值,
f (x)最大值=-( a-
a- a)2+
a)2+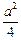 +
+ -
- =
=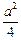 +
+ -
- ……………6分
……………6分
令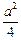 +
+ -
- =1,解得
=1,解得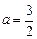 或
或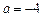 <0(舍去) ……………7分
<0(舍去) ……………7分
③若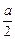 <0,即a<0,则当cosx=0时,f (x)取得最大值,
<0,即a<0,则当cosx=0时,f (x)取得最大值,
f (x)最大值=-(0- a)2+
a)2+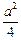 +
+ -
- =
= -
- ……………8分
……………8分
令 -
- =1
=1 ,解得
,解得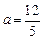 >0(舍去) ……………9分
>0(舍去) ……………9分
综上,存在a=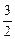 使得f (x)在闭区间
使得f (x)在闭区间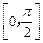 上的最大值为1 ……………10分
上的最大值为1 ……………10分
 -
-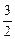
=1-cos2x+acosx+
 -
-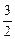 =-cos2x+acosx+
=-cos2x+acosx+ -
-
=-(cosx-
 a)2+
a)2+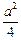 +
+ -
-
∵
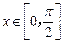 ,∴0≤cos
,∴0≤cos x≤1, ………………1分
x≤1, ………………1分① 若
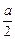 >1,即a>2,则当cosx=1时,f (x)取得最大值,
>1,即a>2,则当cosx=1时,f (x)取得最大值,f (x)最大值=-(1-
 a)2+
a)2+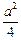 +
+ -
- =
=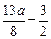 ……………3分
……………3分令
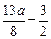 =1,解得
=1,解得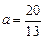 <2(舍去) ……………4分
<2(舍去) ……………4分②若0≤
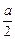 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=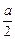 时,f (x)取得最大值,
时,f (x)取得最大值,f (x)最大值=-(
 a-
a- a)2+
a)2+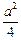 +
+ -
- =
=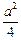 +
+ -
- ……………6分
……………6分令
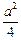 +
+ -
- =1,解得
=1,解得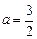 或
或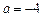 <0(舍去) ……………7分
<0(舍去) ……………7分③若
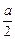 <0,即a<0,则当cosx=0时,f (x)取得最大值,
<0,即a<0,则当cosx=0时,f (x)取得最大值,f (x)最大值=-(0-
 a)2+
a)2+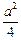 +
+ -
- =
= -
- ……………8分
……………8分令
 -
- =1
=1 ,解得
,解得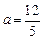 >0(舍去) ……………9分
>0(舍去) ……………9分综上,存在a=
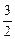 使得f (x)在闭区间
使得f (x)在闭区间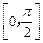 上的最大值为1 ……………10分
上的最大值为1 ……………10分
练习册系列答案
相关题目
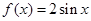 图象按向量
图象按向量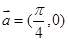 平移得函数
平移得函数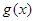 的图象,则函数
的图象,则函数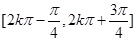 (
(  )
)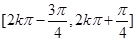 (
(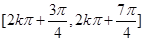 (
(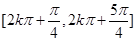 (
(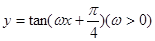 的图像向右平移
的图像向右平移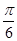 个单位长度后,与函数
个单位长度后,与函数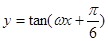 的图像重合,则
的图像重合,则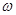 的最小值为( )
的最小值为( )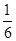
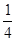
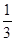
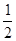
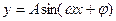 (
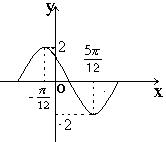
(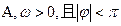 )在一个周期内的图象如右图,
)在一个周期内的图象如右图, 角
角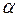 是第三象限角,且
是第三象限角,且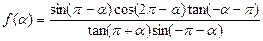
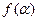 ;
;  2)若
2)若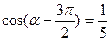 ,求
,求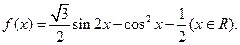
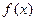 的最小值和最小正周期;
的最小值和最小正周期;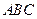 的内角
的内角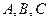 对边分别为
对边分别为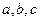 ,且
,且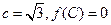 ,
,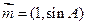 与
与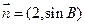 共线,求
共线,求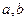 的值.
的值. 是
是  且在[
且在[ ]内有且只有三个零点的函数;
]内有且只有三个零点的函数; 且在[
且在[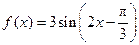 的图象为
的图象为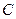 ,则如下结论中正确的序号是 _____
,则如下结论中正确的序号是 _____ 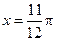 对称;
对称; 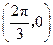 对称;
对称; 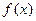 在区间
在区间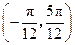 内是增函数;
内是增函数; 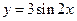 的图角向右平移
的图角向右平移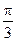 个单位长
个单位长 度可以得到图象
度可以得到图象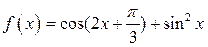
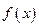 的最大值和最小正周期;
的最大值和最小正周期; 

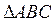 的三个内角,若
的三个内角,若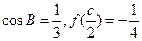 ,且C为锐角,求
,且C为锐角,求