题目内容
某公司研制出一种新型药品,为测试该药品的有效性,公司选定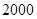 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:
| 分组 | 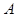 组 组 | 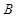 组 组 |  组 组 |
| 药品有效 | 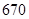 | 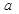 | 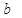 |
| 药品无效 | 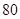 | 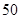 | 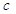 |
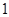 个,抽到
个,抽到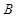 组药品有效的概率是
组药品有效的概率是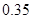 .
.(1)现用分层抽样的方法在全体样本中抽取
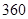 个测试结果,问应在
个测试结果,问应在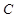 组抽取样本多少个? [来源:学优]
组抽取样本多少个? [来源:学优](2)已知
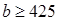 ,
,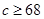 ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于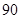 %,则认为测试通过).
%,则认为测试通过).
(1)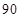 个;(2)通过测试的概率为
个;(2)通过测试的概率为 .
.
解析试题分析:(I)现用分层抽样的方法在全体样本中抽取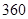 个测试结果,问应在
个测试结果,问应在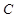 组抽取样本多少个,根据分层抽样的定义,按每层中的比例计算
组抽取样本多少个,根据分层抽样的定义,按每层中的比例计算 组抽取样本的个数,由已知在全体样本中随机抽取
组抽取样本的个数,由已知在全体样本中随机抽取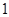 个,抽到
个,抽到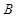 组药品有效的概率是
组药品有效的概率是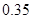 ,即
,即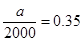 ,可求得
,可求得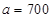 ,可求得
,可求得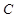 组样本总数
组样本总数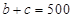 ,从而可求出应在
,从而可求出应在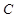 组抽取样本数;(II)由(I)
组抽取样本数;(II)由(I)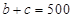 ,再结合题设条件
,再结合题设条件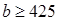 ,
,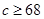 列举出所有可能的
列举出所有可能的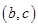 组合的个数及没有通过测试的
组合的个数及没有通过测试的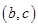 组合的个数,再由概率公式及概率的性质求出通过测试的概率.
组合的个数,再由概率公式及概率的性质求出通过测试的概率.
试题解析:(1)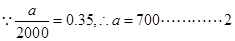 分
分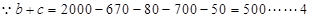 分
分
应在C组抽取样本个数是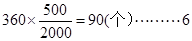 分
分
(2)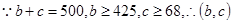 的可能性是
的可能性是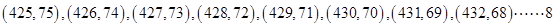 分
分
若测试通过,则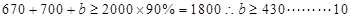 分
分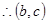 的可能有
的可能有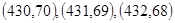
 通过测试的概率为
通过测试的概率为 12分
12分
考点:列举法计算基本事件数及事件发生的概率;分层抽样方法.

练习册系列答案
相关题目
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 | 甲 | 乙 | |||
| 首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
| 每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
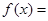
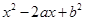 (
(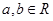 ),若
),若 是从区间
是从区间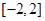 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间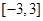 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程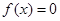 没有实数根的概率.
没有实数根的概率.
 ,
,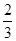 ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.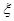 ,求
,求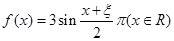 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.
