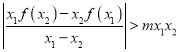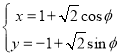题目内容
【题目】已知函数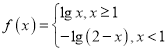 ,
,![]() ,则方程
,则方程![]() 所有根的和等于( )
所有根的和等于( )
A.1B.2C.3D.4
【答案】C
【解析】
证明函数![]() 的图象关于点
的图象关于点![]() 对称,易知函数
对称,易知函数![]() 在定义域
在定义域![]() 上单调递增.由函数
上单调递增.由函数![]() 的图象关于原点
的图象关于原点![]() 对称,得函数
对称,得函数![]() 的图象关于点
的图象关于点![]() 对称,且函数
对称,且函数![]() 在定义域
在定义域![]() 上单调递增. 又
上单调递增. 又![]() 是方程
是方程![]() 的一个根. 当
的一个根. 当![]() 时,令
时,令![]() ,根据零点存在定理和
,根据零点存在定理和![]() 的单调性,知
的单调性,知![]() 在
在![]() 上有且只有一个零点
上有且只有一个零点![]() ,即方程
,即方程![]() 在
在![]() 上有且只有一个根
上有且只有一个根![]() .
.
根据图象的对称性可知方程![]() 在
在![]() 上有且只有一个根
上有且只有一个根![]() ,且
,且![]() .即可求出方程
.即可求出方程![]() 所有根的和.
所有根的和.
设点![]() 是函数
是函数![]() 图象上任意一点,它关于点
图象上任意一点,它关于点![]() 的对称点为
的对称点为![]() ,
,
则![]() ,代入
,代入![]() ,
,
得![]() .
.
![]() 函数
函数![]() 的图象与函数
的图象与函数![]() 的图象关于点
的图象关于点![]() 对称,
对称,
即函数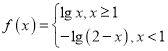 的图象关于点
的图象关于点![]() 对称,易知函数
对称,易知函数![]() 在定义域
在定义域![]() 上单调递增.
上单调递增.
又函数![]() 的图象关于原点
的图象关于原点![]() 对称,
对称,![]() 函数
函数![]() 的图象关于点
的图象关于点![]() 对称,且函数
对称,且函数![]() 在定义域
在定义域![]() 上单调递增.
上单调递增.
又![]() 是方程
是方程![]() 的一个根.
的一个根.
当![]() 时,令
时,令![]() ,则
,则![]() 在
在![]() 上单调递减.
上单调递减.
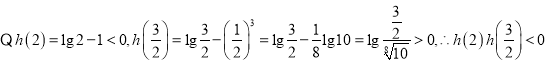 ,
,
根据零点存在定理,可得![]() 在
在![]() 上有一个零点
上有一个零点![]() ,根据
,根据![]() 的单调性知
的单调性知![]() 在
在![]() 上有且只有一个零点
上有且只有一个零点![]() ,即方程
,即方程![]() 在
在![]() 上有且只有一个根
上有且只有一个根![]() .
.
根据图象的对称性可知方程![]() 在
在![]() 上有且只有一个根
上有且只有一个根![]() ,且
,且![]() .
.
故方程![]() 所有根的和等于
所有根的和等于![]() .
.
故选:![]() .
.

【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
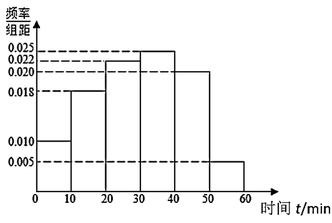
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有10名女生.
类学生中有10名女生.
(1)根据已知条件完成下面![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为达到体育健康
的把握认为达到体育健康![]() 类学生与性别有关?
类学生与性别有关?
非体育健康 | 体育健康 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
|
|
|
|
|
|
|
|
![]()
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 | 90.10% | 4.98% | 3.82% | 1.10% |
净利润占比 | 95.80% |
| 3.82% | 0.86% |
则下列判断中不正确的是( )
A.该公司2018年度冰箱类电器销售亏损
B.该公司2018年度小家电类电器营业收入和净利润相同
C.该公司2018年度净利润主要由空调类电器销售提供
D.剔除冰箱类销售数据后,该公司2018年度空调类电器销售净利润占比将会降低