题目内容
【题目】椭圆
的左右焦点分别为F1，F2，离心率为
，过点F1且垂直于x轴的直线被椭圆截得的弦长为
，直线l：y=kx+m与椭圆交于不同的A，B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若在椭圆C上存在点Q满足： 
（O为坐标原点）．求实数λ的取值范围．
【答案】（Ⅰ）
；（Ⅱ）
．
【解析】试题分析：（Ⅰ）由已知得
，又
，联立解得即可；（II）设A
，B
，Q
，分类讨论：当λ=0时，利用椭圆的对称性即可得出；λ≠0时，设直线AB的方程为y=kx+m．与椭圆的方程联立得到△＞0及根与系数的关系，再利用向量相等，代入计算即可得出
试题解析：（Ⅰ）由已知得
，
解得
所以椭圆Ｃ的方程为
．
（Ⅱ）设
， 
， 
当
时由
知， 
，Ａ与Ｂ关于原点对称，存在Ｑ满足题意
成立．
当
时， 
得
得
， 
由
，得
， 
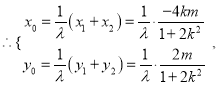
代入到得
代入（＊）式
，由
得
且
．
综上
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
