Question

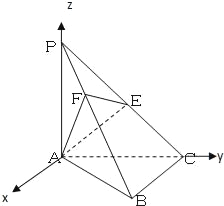
【题目】已知在三棱锥P﹣ABC中，PA⊥面ABC，AC⊥BC，且PA=AC=BC=1，点E是PC的中点，作EF⊥PB交PB于点F．

（Ⅰ）求证：PB⊥平面AEF；

（Ⅱ）求二面角A﹣PB﹣C的大小．

Answer 1

【答案】（Ⅰ）见解析；（2）60°．

【解析】试题分析：

（Ⅰ）要证直线PB与平面AEF垂直，就要证PB与平面AEF内两条相交直线垂直，其中已知有一个垂直：EF⊥PB，由等腰三角形性质知AE⊥PC，因此可先证AE⊥平面PBC得AE⊥PB，这又可通过证明BC⊥平面PAC得到；（Ⅱ）要求二面角大小，由图可建立空间直角坐标系（见解析），写出各点坐标，求出二面角两个面的法向量，由法向量夹角得二面角（相等或互补）．

试题解析：

（Ⅰ）证明：∵PA⊥面ABC，BC面ABC，

∴PA⊥BC，又AC⊥BC，PA⊥BC，PA∩AC=A，∴BC⊥面PAC，

而AEPAC，∴BC⊥AE，又PA=AC，点E是PC的中点，∴AE⊥PC，

又AE⊥BC，BC∩PC=C，∴AE⊥面PBC，而PB面PBC，AE⊥PB，又EF⊥PB，AE⊥BP，AE∩EF=E，∴PB⊥平面AEF；

（Ⅱ）解：以A为坐标原点，AC所在直线为y轴，AP所在直线为z轴建立空间直角坐标系，

∵PA=AC=BC=1，则A（0，0，0），P（0，0，1），C（0，1，0），B（1，1，0）．

．

设平面PAB的一个法向量为，

则由，得，取y1=﹣1，得x1=1，z1=0，

∴．

再设平面PBC的一个法向量为，

则由，得，取z2=1，得y2=1，

∴．

∴．

∴二面角A﹣PB﹣C的大小为60°．