题目内容
(本小题满分12分)
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组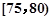 ,第2组
,第2组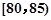 ,第3组
,第3组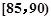 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.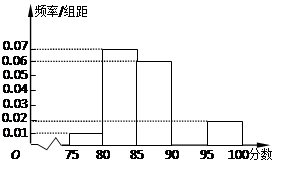
(1)求出第4组的频率;
(2)如果用分层抽样的方法从“优秀”和“良好” 的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(1)0.2(2)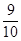
解析试题分析:(Ⅰ)其它组的频率为(0.01+0.07+0.06+0.02)×5="0." 8,所以第四组的频率为0.2,…5分
(Ⅱ)依题意良好的人数为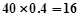 人,优秀的人数为
人,优秀的人数为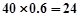 人
人
优秀与良好的人数比为3:2,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,记从这5人中选2人至少有1人是优秀为事件M, 将考试成绩优秀的三名学生记为A,B,C,考试成绩良好的两名学生记为a,b 从这5人中任选2人的所有基本事件包括:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,ab共10个基本事件
事件M含的情况是:AB,AC,BC,Aa,Ab,Ba,Bb,Ca,Cb,共9个
所以 ………12分
………12分
考点:频率分布直方图与分层抽样古典概率
点评:频率分布直方图中各矩形面积和为1,每一个小矩形的面积代表该组的频率,分层抽样是各层按照所占样本容量的比例抽取,古典概率需要找到所有基本事件总数及满足某一条件的基本事件数目,然后求其比值

下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据。
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
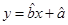 ;
;(2)已知该厂技改前100吨甲产品生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考公式:
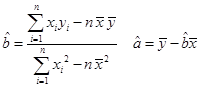 )
) (本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个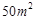 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 | 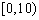 | 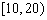 | 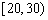 | 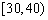 | 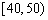 |
| 频数 | 10 | 35 | 40 | 10 | 5 |
| 小麦产量 | 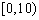 | 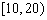 | 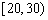 | 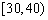 |
| 频数 | 15 | 50 | 30 | 5 |
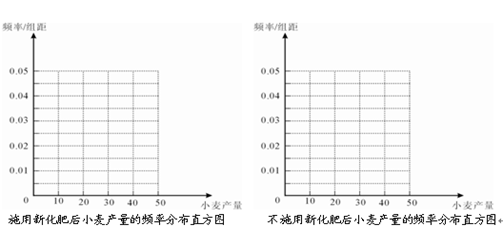
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
| | 小麦产量小于20kg | 小麦产量不小于20kg | 合计 |
| 施用新化肥 | 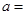 | 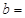 | |
| 不施用新化肥 | 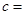 |  | |
| 合计 | | | 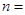 |
附:
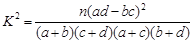
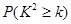 | 0.050 | 0.010 | 0.005 | 0.001 |
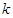 | 3.841 | 6.635 | 7.879 | 10.828 |
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 | 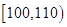 | 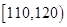 | 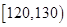 | 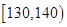 | 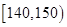 |
| 人数 | 4 | 8 |  | 5 | 3 |
| 生产能力分组 | 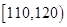 | 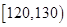 | 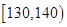 | 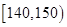 |
| 人数 | 6 | y | 36 | 18 |
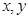 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
(2)分别估计
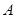 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1) 
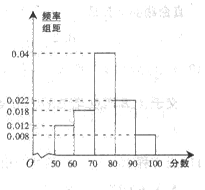

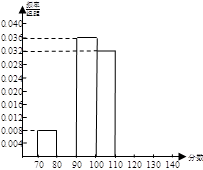
 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为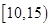 ,
,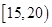 ,
,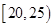 ,
,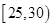 ,
,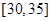 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在
 名
名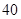 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共 人,患胃病者生活规律的共
人,患胃病者生活规律的共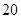 人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共
人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共 人.
人.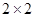 列联表.
列联表.