题目内容
已知函数y=f(x)是定义在区间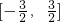 上的偶函数,且
上的偶函数,且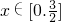 时,f(x)=-x2-x+5
时,f(x)=-x2-x+5
(1)求函数f(x)的解析式;
(2)将函数g(x)=-x2-x+5,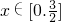 的图象按向量a=(1,b)(b∈R)平移得到函数h(x)的图象,求函数h(x)的解析式并解不等式h(x)<0.
的图象按向量a=(1,b)(b∈R)平移得到函数h(x)的图象,求函数h(x)的解析式并解不等式h(x)<0.
解(1)当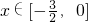 时,-x∈
时,-x∈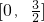 ∴f(-x)=-(-x2)-(-x)+5=-x2+x+5
∴f(-x)=-(-x2)-(-x)+5=-x2+x+5
∵f(x)是偶函数,∴f(-x)=f(x)∴f(x)=-x2+x+5,x∈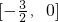
∴f(x)=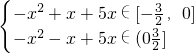
(2)依题意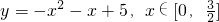 ①
①
将y′=y+b,x′=x+1代入①得 y-b=-(x'-1)2-(x'-1)+52 且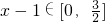
∴h(x)=-x2+x+5+b且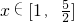
由h(x)<0 b<x2-x-5
b<x2-x-5
设y1=by2=x2-x-5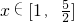
易知y2在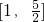 ↑,
↑,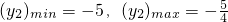
则当b<-5时,解集为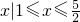 ,当b=-5时,解集{x|1<
,当b=-5时,解集{x|1<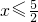
当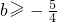 时,解集为φ;
时,解集为φ;
当-5<b< 时,由x2-x-5-b=0解的
时,由x2-x-5-b=0解的 (舍)
(舍)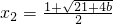
解集为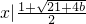 <
<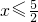
分析:(1)根据偶函数的定义可知先求出函数在区间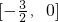 上的函数解析式,从而求出函数y=f(x)在区间
上的函数解析式,从而求出函数y=f(x)在区间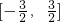 上的解析式;
上的解析式;
(2)先根据向量平移求出函数h(x)的解析式,然后讨论b的范围,分别求出不等式h(x)<0的解集.
点评:本题综合考查了函数的基本性质,已知奇偶性求函数解析式的问题,以及图象的平移和解不等式,属于中档题.
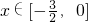 时,-x∈
时,-x∈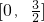 ∴f(-x)=-(-x2)-(-x)+5=-x2+x+5
∴f(-x)=-(-x2)-(-x)+5=-x2+x+5∵f(x)是偶函数,∴f(-x)=f(x)∴f(x)=-x2+x+5,x∈
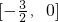
∴f(x)=
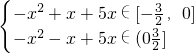
(2)依题意
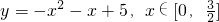 ①
①将y′=y+b,x′=x+1代入①得 y-b=-(x'-1)2-(x'-1)+52 且
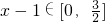
∴h(x)=-x2+x+5+b且
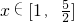
由h(x)<0
 b<x2-x-5
b<x2-x-5设y1=by2=x2-x-5
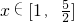
易知y2在
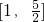 ↑,
↑,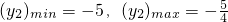
则当b<-5时,解集为
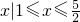 ,当b=-5时,解集{x|1<
,当b=-5时,解集{x|1<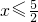
当
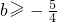 时,解集为φ;
时,解集为φ;当-5<b<
 时,由x2-x-5-b=0解的
时,由x2-x-5-b=0解的 (舍)
(舍)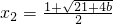
解集为
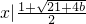 <
<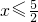
分析:(1)根据偶函数的定义可知先求出函数在区间
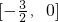 上的函数解析式,从而求出函数y=f(x)在区间
上的函数解析式,从而求出函数y=f(x)在区间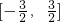 上的解析式;
上的解析式;(2)先根据向量平移求出函数h(x)的解析式,然后讨论b的范围,分别求出不等式h(x)<0的解集.
点评:本题综合考查了函数的基本性质,已知奇偶性求函数解析式的问题,以及图象的平移和解不等式,属于中档题.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足