题目内容
16.某生产厂家根据市场调查分析,决定调整产品生产方案,准备每周(按5天计算)生产A,B,C三种产品共15吨(同一时间段内只能生产一种产品),已知生产这些产品每吨所需天数和每吨产值如表:| 产品名称 | A | B | C |
| 天 | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值(单位:万元) | 4 | $\frac{7}{2}$ | 2 |
| A. | 30 | B. | 40 | C. | 47.5 | D. | 52.5 |
分析 设出每周生产A,B产品的吨数,得到生产C成品的吨数,建立约束条件和目标函数,利用线性规划的知识即可得到结论.
解答 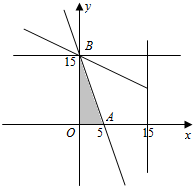 解:
解:
设每周生产A产品x吨,B产品y吨,则生产C产品15-x-y吨,产值为z.
目标函数为z=4x+$\frac{7}{2}$y+2(15-x-y)=2x+$\frac{3}{2}$y+30,
题目中包含的约束条件为:
$\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y+\frac{1}{4}(15-x-y)≤5}\\{0≤15-x-y≤15}\\{0≤x≤15}\\{0≤y≤15}\end{array}\right.$,即$\left\{\begin{array}{l}{3x+y-15≤0}\\{0≤x+y≤15}\\{0≤x≤15}\\{0≤y≤15}\end{array}\right.$
可行域如图所示:
化目标函数z=2x+$\frac{3}{2}$y+30为$y=-\frac{4}{3}x+\frac{z}{3}-20$.
由图可知,当直线$y=-\frac{4}{3}x+\frac{z}{3}-20$过B(0,15)时,直线在y轴上的截距最大,
z有最大值为$2×0+\frac{3}{2}×15+30=52.5$.
故选:D.
点评 本题主要考查线性规划的应用,建立约束条件和目标函数是解决本题的关键,是中档题.

练习册系列答案
相关题目
4.某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.
甲说:我在1日和3日都有值班;
乙说:我在8日和9日都有值班;
丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是( )
甲说:我在1日和3日都有值班;
乙说:我在8日和9日都有值班;
丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是( )
| A. | 2日和5日 | B. | 5日和6日 | C. | 6日和11日 | D. | 2日和11日 |
11.已知A={x|x>1},B={x|x2-2x<0},则A∪B=( )
| A. | {x|x<0或x≥1} | B. | {x|1<x<2} | C. | {x|x<0或x>1} | D. | {x|x>0} |
6.各项都为正数的等比数列{an}的前n项和为Sn,若S3=32,a5+a6+a7=2,则公比的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
 如图,已知圆B的半径为5,直线AMN与直线ADC为圆B的两条割线,且割线AMN过圆心B.若AM=2,∠CBD=60°,则AD=3.
如图,已知圆B的半径为5,直线AMN与直线ADC为圆B的两条割线,且割线AMN过圆心B.若AM=2,∠CBD=60°,则AD=3.