题目内容

8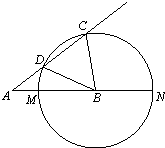．如图，已知圆B的半径为5，直线AMN与直线ADC为圆B的两条割线，且割线AMN过圆心B．若AM=2，∠CBD=60°，则AD=3．

分析 利用△CDB是等边三角形，求出CD，再利用割线定理，即可求出AD．

解答 解：由题意，CD=DB=BC=5，AN=12，
∵直线AMN与直线ADC为圆B的两条割线，
∴AD×（AD+5）=2×12，
∴AD2+5AD-24=0，
∴AD=3，
故答案为：3．

点评 本题考查割线定理，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
18．已知三次函数f（x）=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2-6x+1（x∈R），a，b为实数．
（1）若a=3，b=3时，求函数f（x）的极大值和极小值；
（2）设函数g（x）=f′（x）+7有唯一零点，若b∈[1，3]，求g（1）的取值范围．
19．若实数x，y满足4x-y2=0，则$\frac{y}{x+1}$的取值范围为-1≤t≤1．
16．某生产厂家根据市场调查分析，决定调整产品生产方案，准备每周（按5天计算）生产A，B，C三种产品共15吨（同一时间段内只能生产一种产品），已知生产这些产品每吨所需天数和每吨产值如表：
产品名称ABC
天$\frac{1}{2}$$\frac{1}{3}$$\frac{1}{4}$
产值（单位：万元）4$\frac{7}{2}$2
则每周最高产值是（　　）
A．30B．40C．47.5D．52.5
3．执行如图所示的程序框图，则输出的n的值是（　　）
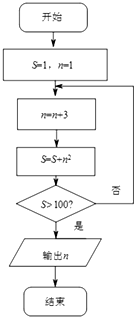
A．7B．10C．66D．166
13．若2x+5y≤2-y+5-x，则有x+y≤0．
20．在平面直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}x=rcosα\\ y=rsinα\end{array}\right.$（α为参数，r为常数，r＞0）．以原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为$\sqrt{2}ρcos（θ+\frac{π}{4}）+2=0$．若直线l与曲线C交于A，B两点，且$AB=2\sqrt{2}$，求r的值．
17．已知函数y=f（x）的图象经过坐标原点，且f（x）=x2-x+b，数列{an}的前n项和Sn=f（n）（n∈N*）．
（1）求数列{an}的通项公式；
（2）设Pn=a1+a4+a7+…+a3n-2，Qn=a10+a12+a14+…+a2n+8，其中n∈N*，试比较Pn与Qn的大小，并证明你的结论；
（3）若数列{bn}满足an+log3n=log3bn，求数列{bn}的前n项和Tn．
18．设x，y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x≤2}\\{y≥1}\end{array}\right.$，则z=x-2y的最小值是（　　）
A．-6B．-3C．0D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网