题目内容
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
【答案】(Ⅰ)见解析;(Ⅱ)池底设计为边长![]() 米的正方形时,总造价最低,其值为
米的正方形时,总造价最低,其值为![]() 元.
元.
【解析】试题分析:(Ⅰ)由长方体的容积除以深度可得池底的面积,用池底面积除以长方形的长可得池底长方形的宽.池壁面积等于池底长方开的周长乘以池子的高底;(Ⅱ)用池底的单价与池壁的单价各自乘以面积后求和,可得总造价的关系式,再利用基本不等式求出![]() 为何值时,总造价最低.
为何值时,总造价最低.
试题解析:(Ⅰ)设水池的底面积为S1,池壁面积为S2,
则有![]() (平方米).池底长方形宽为
(平方米).池底长方形宽为![]() 米,则
米,则
S2=8x+8×![]() =8(x+
=8(x+![]() ).
).
(Ⅱ)设总造价为y,则
y=120×1 600+100×8![]() ≥192000+64000=256000.当且仅当x=
≥192000+64000=256000.当且仅当x=![]() ,即x=40时取等号.
,即x=40时取等号.
所以x=40时,总造价最低为256000元.
答:当池底设计为边长40米的正方形时,总造价最低,其值为256000元.

【题目】某大学餐饮中心为了了解新生的饮食习惯,利用简单随机抽样的方法在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)根据(1)的结论,你能否提出更好的调查方法来了解该校大学新生的饮食习惯,说明理由.
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
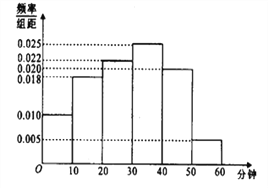
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(参考公式![]() ,其中
,其中![]() .)
.)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率。