Question

2．△ABC内接于单位圆，三个内角A，B，C的平分线延长后分别交此圆于A₁，B₁，C₁，则$\frac{A{A}_{1}•cos\frac{A}{2}+B{B}_{1}•cos\frac{B}{2}+C{C}_{1}•cos\frac{C}{2}}{sinA+sinB+sinC}$=2．

Answer 1

分析 首先，根据题意，画出图形，然后，连BA₁，则AA₁=2sin（B+$\frac{A}{2}$），然后，根据三角形的内角平分线和内角和定理，化简关系式，得到AA₁cos$\frac{A}{2}$=2cos（$\frac{B}{2}-\frac{C}{2}$）cos$\frac{A}{2}$=sinC+sinB，同理，得到BB₁cos$\frac{B}{2}$=sinA+sinC，CC₁cos$\frac{C}{2}$=sinA+sinB，然后，求解即可．

解答 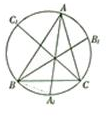解：如图所示，连BA₁，则AA₁=2sin（B+$\frac{A}{2}$）
=2sin（$\frac{A+B+C}{2}+\frac{B}{2}-\frac{C}{2}$）
=2cos（$\frac{B}{2}-\frac{C}{2}$）
∴AA₁cos$\frac{A}{2}$=2cos（$\frac{B}{2}-\frac{C}{2}$）cos$\frac{A}{2}$
=cos$\frac{A+B-C}{2}$+cos$\frac{A+C-B}{2}$
=cos（$\frac{π}{2}-C$）+cos（$\frac{π}{2}-B$）
=sinC+sinB，
同理，得
BB₁cos$\frac{B}{2}$=sinA+sinC
CC₁cos$\frac{C}{2}$=sinA+sinB
∴AA₁cos$\frac{A}{2}$+BB₁cos$\frac{B}{2}$+CC₁cos$\frac{C}{2}$=2（sinA+sinB+sinC）
∴$\frac{A{A}_{1}•cos\frac{A}{2}+B{B}_{1}•cos\frac{B}{2}+C{C}_{1}•cos\frac{C}{2}}{sinA+sinB+sinC}$
=2．
故答案为：2．

点评 本题重点考查了三角形的基本性质、三角公式等、属于难题．