题目内容
已知函数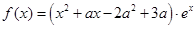 ,其中
,其中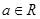 .
.
(1)是否存在实数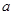 ,使得函数
,使得函数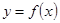 在
在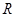 上单调递增?若存在,求出的
上单调递增?若存在,求出的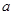 值或取值范围;否则,请说明理由.
值或取值范围;否则,请说明理由.
(2)若a<0,且函数y=f(x)的极小值为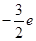 ,求函数的极大值。
,求函数的极大值。
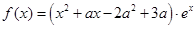 ,其中
,其中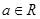 .
.(1)是否存在实数
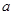 ,使得函数
,使得函数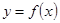 在
在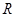 上单调递增?若存在,求出的
上单调递增?若存在,求出的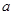 值或取值范围;否则,请说明理由.
值或取值范围;否则,请说明理由.(2)若a<0,且函数y=f(x)的极小值为
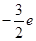 ,求函数的极大值。
,求函数的极大值。(1)存在a=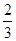 ;(2)
;(2)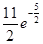 .
.
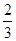 ;(2)
;(2)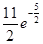 .
.试题分析:(1)利用导数求得函数单调递增
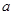 满足的条件;(2)先求出函数的两个极值点,根据a<0确定极大值与极小值点,由函数的极小值求得
满足的条件;(2)先求出函数的两个极值点,根据a<0确定极大值与极小值点,由函数的极小值求得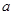 ,再求出极大值.
,再求出极大值.(1)∵
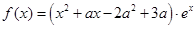 ,
,∴
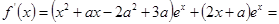
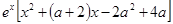 .
.由
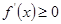 可得
可得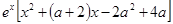 ≥0.即
≥0.即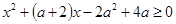 在x∈R时恒成立.
在x∈R时恒成立.∴Δ=(a+2)2-4(-2a2+4a)≤0,即(3a-2)2≤0,即a=
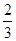 ,此时,f′(x)=(x+
,此时,f′(x)=(x+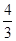 )2ex≥0,函数y=f(x)在R上单调递增.(2)由f′(x)=0可得ex[x2+(a+2)x-2a2+4a]=0,解之得x1=-2a,x2=a-2.
)2ex≥0,函数y=f(x)在R上单调递增.(2)由f′(x)=0可得ex[x2+(a+2)x-2a2+4a]=0,解之得x1=-2a,x2=a-2.当a<0时,-2a>a-2,当x变化时,f′(x),f(x)的变化情况如下:
| x | (-∞,a-2) | a-2 | (a-2,-2a) | -2a | (-2a,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
由条件可知,f(-2a)=-
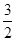 e,即3a·e-2a=-
e,即3a·e-2a=-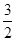 e,
e,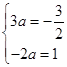 可得a=-
可得a=-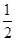 .
.此时,f(x)=(x2-
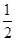 x-2)ex,极大值为f(a-2)=f(-
x-2)ex,极大值为f(a-2)=f(-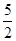 )=
)=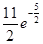 .
.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
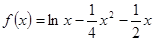 .
.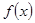 的单调区间和极值;
的单调区间和极值;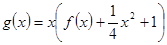 ,当
,当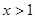 时,
时,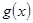 在区间
在区间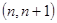 内存在极值,求整数
内存在极值,求整数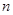 的值.
的值.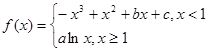
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点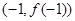 处的切线的斜率是
处的切线的斜率是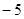 .
.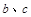 的值;
的值;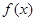 在区间
在区间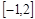 上的最大值;
上的最大值;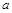 ,曲线
,曲线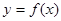 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得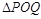 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在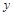 轴上?说明理由.
轴上?说明理由.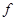 (
(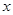 ) =
) =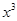 ,g (
,g (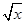 。
。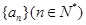 满足
满足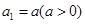 ,
,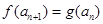 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的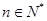 ,都有
,都有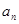 ≤
≤ 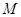 .
.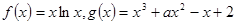
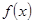 的单调区间;
的单调区间;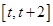
 上的最小值;
上的最小值;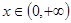 ,
,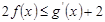 恒成立,求实数
恒成立,求实数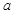 的取值范围.
的取值范围.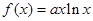 ,
,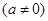 .
.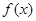 的单调区间;
的单调区间;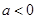 时,若对于任意的
时,若对于任意的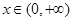 ,都有
,都有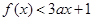 成立,求
成立,求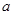 的取值范围.
的取值范围. ,g(x)=
,g(x)=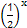 -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.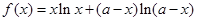
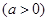 .
.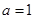 时,求函数
时,求函数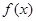 的最小值;
的最小值; ,都有
,都有 ;
;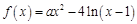 ,
,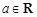 .
.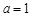 时,求
时,求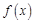 的单调区间;
的单调区间;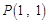 和函数
和函数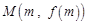 ,对任意
,对任意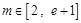 ,直线
,直线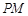 倾斜角都是钝角,求
倾斜角都是钝角,求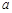 的取值范围.
的取值范围.