题目内容
设 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, .若对任意的
.若对任意的 ,不等式
,不等式 恒成立, 求实数
恒成立, 求实数 的取值范围
的取值范围
 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, .若对任意的
.若对任意的 ,不等式
,不等式 恒成立, 求实数
恒成立, 求实数 的取值范围
的取值范围 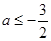
试题分析: 不等式恒成立问题,先化简不等式.本题是一个分段函数
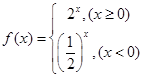 ,需分类讨论,以便确定对应解析式. 当
,需分类讨论,以便确定对应解析式. 当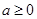 时,
时,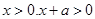 即有
即有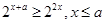 ,不合.当
,不合.当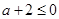 时,
时,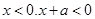 即有
即有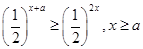 ,符合. 当
,符合. 当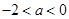 且
且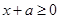 时,
时,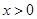 则
则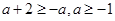 ,不合. 当
,不合. 当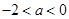 且
且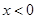 时,
时,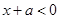 ,符合. 当
,符合. 当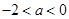 且
且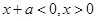 时,
时, 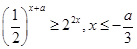 ,所以
,所以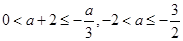 .综合并集得
.综合并集得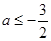 .
.试题解析:
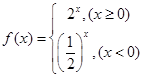 4分
4分当
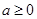 时,即有
时,即有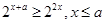 ,不合 6分
,不合 6分当
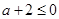 时,即有
时,即有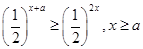 ,恒成立,
,恒成立,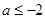 符合 8分
符合 8分当
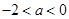 时,若
时,若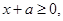 则
则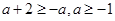 由(1)得不合
由(1)得不合若
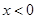 由(2)得成立,则
由(2)得成立,则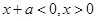 时恒成立,即
时恒成立,即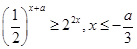
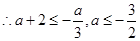 ,
, 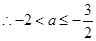 14分
14分实数
 的取值范围
的取值范围
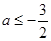 15分
15分
练习册系列答案
相关题目
 R.
R. .
. ,
, ,
, .
. 时,恒有
时,恒有 ,求
,求 的最大值;
的最大值; 时,恒有
时,恒有 ,求
,求 ,B={x/ax2+bx+c
,B={x/ax2+bx+c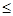 0},若
0},若 则
则 的最小值_______.
的最小值_______. ,若集合
,若集合 中的元素个数为
中的元素个数为 ,则实数
,则实数 的取值范围为 .
的取值范围为 . >a>b>1,则f(a),f(b),f(c)比较大小关系正确的是( ).
>a>b>1,则f(a),f(b),f(c)比较大小关系正确的是( ).
