题目内容
6．计算由直线y=2x-1，曲线y=$\sqrt{x}$以及x轴所围成的封闭图形的面积S．分析 根据定积分的几何意义，先求出积分的上下限，即可求出所围成的图形的面积．
解答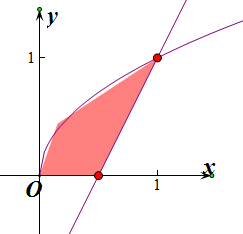 
解：联立直线y=2x-1，曲线y=$\sqrt{x}$构成方程组$\left\{\begin{array}{l}{y=2x-1}\\{y=\sqrt{x}}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，
联立直线y=2x-1，y=0构成方程组，解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=0}\end{array}\right.$
∴直线y=2x-1，曲线y=$\sqrt{x}$以及x轴所围成的封闭图形的面积S=${∫}_{0}^{1}$$\sqrt{x}$dx-${∫}_{\frac{1}{2}}^{1}$（2x-1）dx=$\frac{2}{3}{x}^{\frac{3}{2}}$|${\;}_{0}^{1}$-（x2-x）|${\;}_{\frac{1}{2}}^{1}$=$\frac{2}{3}$-$\frac{1}{4}$=$\frac{5}{12}$
点评 本题考查了定积分的几何意义，关键是求出积分的上下限，属于基础题．
练习册系列答案
相关题目
16．已知A（1，0），曲线C：y=eax恒过点B，若P是曲线C上的动点，且$\overrightarrow{AB}$•$\overrightarrow{AP}$的最小值为2，则a的值为（ ）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |
14．过点（3，-1），圆心在y轴上，且与x轴相切的圆的方程为（ ）
| A． | x2+y2-10y=0 | B． | x2+y2+10y=0 | C． | x2+y2+10x=0 | D． | x2+y2-10x=0 |
1．给出演绎推理的“二段论”，已知函数f（x）=$\frac{1}{x}$在（-∞，0）∪（0，+∞）是单调递减的，有因为-1＜2，所以f（-1）＞f（2），即-1$＞\frac{1}{2}$，这显然是不对的，那么这个推理是（ ）
| A． | 大前提推理 | B． | 小前提推理 | C． | 推理形式错误 | D． | 非以上错误 |
11．与-$\frac{π}{6}$角终边相同的角是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{11π}{6}$ | D． | $\frac{4π}{3}$ |