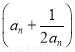题目内容
设函数f(x)＝sin(ωx＋φ)＋cos(ωx＋φ) 
的最小正周期为π，且f(－x)＝f(x)，则( )．
A．f(x)在
单调递减 B．f(x)在
单调递减
C．f(x)在
单调递增 D．f(x)在
单调递增
A
【解析】f(x)＝sin(ωx＋φ)＋cos(ωx＋φ)＝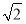
sin
.
由最小正周期为π得ω＝2，
又由f(－x)＝f(x)可知f(x)为偶函数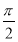，|φ|＜
可知φ＝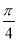
，所以f(x)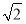＝cos2x在
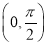单调递减．
练习册系列答案
相关题目
