Question

【题目】已知平面内一个动点M到定点F(3，0)的距离和它到定直线l：x=6的距离之比是常数．

(1)求动点M的轨迹T的方程；

(2)若直线l：x+y-3=0与轨迹T交于A，B两点，且线段AB的垂直平分线与T交于C，D两点，试问A，B，C，D是否在同一个圆上?若是，求出该圆的方程；若不是，说明理由．

Answer 1

【答案】（1）；（2）四点共圆，圆方程为.

【解析】

（1）按求轨迹方法，把条件用数学关系式表示，化简，即可求解；

（2）先求出直线与椭圆交点坐标，再求出直线垂直平分线方程，若四点共圆，此圆以为直径，故只需证明中点与的距离是否等于.

（1）设是点到直线的距离，的坐标为，

由题意，所求的轨迹集合是，

由此得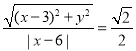，化简得T：；

（2）将直线方程与椭圆方程联立，由，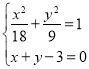

得，中点，

的垂直平分线方程为，

由消去得，

设，则，

，

设线段的中点为，则，

，所以，

，

所以四点在以为圆心，以为半径的圆上，

此圆方程为.