Question

【题目】请解答以下问题，要求解决两个问题的方法不同.

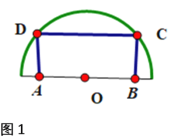
（1）如图1，要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形，如何截取？并求出这个最大矩形的面积.

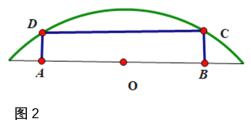
（2）如图2，要在一个长半轴为2米，短半轴为1米的半个椭圆铁板中截取一块面积最大的矩形，如何截取？并求出这个最大矩形的面积.

Answer 1

【答案】（1），面积最大为1（2），，面积最大值为2

【解析】

（1）通过设出∠BOC＝α，进而用α表示出OB，BC；最后表示出S利用三角函数即可求解；

（2）通过设出点C的坐标（m，n），进而表示出OB＝m，BC＝n，S＝2mn；再利用点C为椭圆上的点，即满足其方程利用基本不等式求解即可；

（1）设∠BOC＝α，（）；

∴OB＝cosα，BC＝sinα；

∵S＝2OBBC，

∴S═2sinαcosα＝sin2α；

∴当时，即OA时，矩形面积最大为1；

（2）依题意可得：椭圆方程为：；

设：点C坐标为（m，n）即：OB＝m，BC＝n；

∴S＝2OBBC＝2mn；

∵点C为椭圆上的点；

∴；

∵；

∴mn≤1，当且仅当时取等号；

∴S≤2；即矩形面积最大为2；当OB，即时取等号；