题目内容
【题目】已知函数![]() 定义在区间
定义在区间![]() 内,对于任意的
内,对于任意的![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() .
.
(1)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(2)判断这样的函数是否具有奇偶性和单调性,并加以证明;
(3)若![]() ,求方程
,求方程![]() 的解.
的解.
【答案】(1)满足;(2)奇函数、减函数;(3)![]() .
.
【解析】
试题分析:(1)由![]() 得定义域为
得定义域为![]() .通过对数运算可得
.通过对数运算可得![]() 成立,由
成立,由![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
(2)令![]()
![]()
![]() ,再令
,再令![]()
![]()
![]()
![]()
![]() 函数
函数![]() 为奇函数.任取
为奇函数.任取![]() ,且
,且 ![]() ,证明
,证明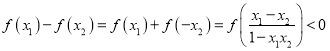 成立
成立![]()
![]() 在区间
在区间![]() 内是减函数;
内是减函数;
(3)利用奇偶性和已知等式可将方程化为![]() ,再根据单调性可得
,再根据单调性可得![]()
![]() 方程的解为
方程的解为![]() .
.
试题解析:(1)![]()
![]() ,
,![]()
![]() ,
,
即定义域为![]() .
.
又![]() ,
,
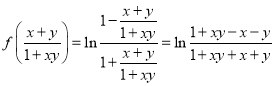 ,
,
![]()
![]() 成立,
成立,
且![]() 时,
时,![]() ,即
,即![]() ,∴
,∴![]() .
.
即![]() ,符合条件
,符合条件
(2)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
![]()
![]() ,即函数
,即函数![]() 为奇函数.
为奇函数.
任取![]() ,且
,且 ![]() ,
,
则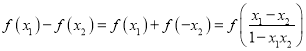 .
.
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() ,则
,则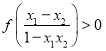 ,
,
即![]() .
.
![]()
![]() 在区间
在区间![]() 内是减函数
内是减函数
(3)![]()
![]() 为奇函数,
为奇函数,
![]()
![]() ,
,
又![]() ,
,
且![]() ,
,
![]()
![]() ,
,![]() .
.
![]()
![]() .
.
![]()
![]() 在区间
在区间![]() 内是单调函数,
内是单调函数,
![]()
![]() .即
.即![]() (舍).
(舍).
故方程的解为![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目