题目内容
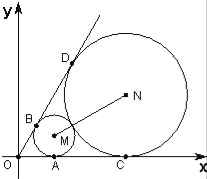
【题目】如图,已知圆心坐标为(![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y=![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=![]() x分别相切于C、D两点.
x分别相切于C、D两点.
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
试题分析:(1)圆M的圆心已知,且其与x轴及直线![]() 分别相切于A,B两点,故半径易知,另一圆N与圆M外切、且与x轴及直线
分别相切于A,B两点,故半径易知,另一圆N与圆M外切、且与x轴及直线![]() 分别相切于C、D两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可;(2)本题研究的是直线与圆相交的问题,由于B点位置不特殊,故可以由对称性转化为求过A点且与线MN平行的线被圆截得弦的长度,下易解
分别相切于C、D两点,由相似性易得其圆心坐标与半径,依定义写出两圆的方程即可;(2)本题研究的是直线与圆相交的问题,由于B点位置不特殊,故可以由对称性转化为求过A点且与线MN平行的线被圆截得弦的长度,下易解
试题解析:(1)由于⊙M与∠BOA的两边均相切,故M到OA及OB的距离均为⊙M的半
径,则M在∠BOA的平分线上,
同理,N也在∠BOA的平分线上,即O,M,N三点共线,且OMN为∠BOA
的平分线,
∵M的坐标为(![]() ,1),∴M到x轴的距离为1,即⊙M的半径为1,
,1),∴M到x轴的距离为1,即⊙M的半径为1,
则⊙M的方程为![]() ,
,
设⊙N的半径为r,其与x轴的切点为C,连接MA,NC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,
即![]() 得r=3,
得r=3,
则OC=![]() ,则⊙N的方程为
,则⊙N的方程为![]() ;
;
(2)由对称性可知,所求的弦长等于过A点直线MN的平行线被⊙N截得的弦的长度,
此弦的方程是![]() ,即:x﹣
,即:x﹣![]() ﹣
﹣![]() =0,
=0,
圆心N到该直线的距离d=![]() ,则弦长=2
,则弦长=2![]() .
.

练习册系列答案
相关题目