Question

【题目】销售甲、乙两种商品所得利润分别是万元，它们与投入资金万元的关系分别为（其中都为常数），函数对应的曲线如图所示.

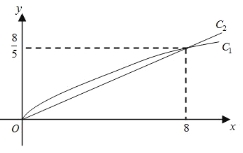
（1）求函数的解析式；

（2）若该商场一共投资8万元经销甲、乙两种商品，求该商场所获利润的最大值.

Answer 1

【答案】（1），（2）万元.

【解析】

试题分析：（1）根据所给的图象知，两曲线的交点坐标为（8，），由此列出关于m，a的方程组，解出m，a的值，即可得到函数的解析式；（2）对甲种商品投资x（万元），对乙种商品投资（8-x）（万元），根据公式可得甲、乙两种商品的总利润y（万元）关于x的函数表达式；再利用配方法确定函数的对称轴，结合函数的定义域，即可求得总利润y的最大值

试题解析：（1）由题意，解得，

又由题意得

（2）设销售甲商品投入资金万元，则乙投入（）万元

由（1）得，

令，则有

当即时,取最大值

答：该商场所获利润的最大值为万元.