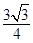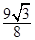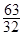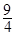题目内容
已知点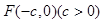 是双曲线
是双曲线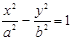 的左焦点,离心率为
的左焦点,离心率为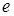 ,过
,过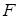 且平行于双曲线渐近线的直线与圆
且平行于双曲线渐近线的直线与圆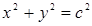 交于点
交于点 ,且点
,且点 在抛物线
在抛物线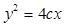 上,则
上,则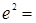 ( )
( )
A.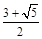 | B.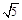 | C.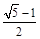 | D.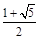 |
D
解析试题分析:如图,设抛物线y2=4cx的准线为l,作PQ⊥l于Q,
双曲线的右焦点为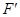 ,由题意可知F
,由题意可知F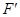 为圆x2+y2=c2的直径,
为圆x2+y2=c2的直径,
∴设P(x,y),(x>0),则P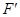 ⊥PF,且tan∠PFF′=
⊥PF,且tan∠PFF′=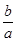 ,
,
∴满足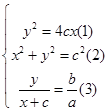 ,将(1)代入(2)得x2+4cx-c2=0,则x=
,将(1)代入(2)得x2+4cx-c2=0,则x=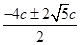 =-2c
=-2c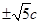 ,
,
即x= ,或x=
,或x= (舍去)
(舍去)
将x= 代入③,得
代入③,得 ,即y=
,即y= ,再将y代入①得,
,再将y代入①得,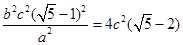 ,即
,即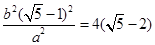 ),
),
∴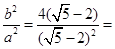
 ,即e2=1+
,即e2=1+ =
=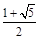 .故选D.
.故选D.
考点:双曲线的简单性质.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
(5分)(2011•湖北)将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( )
| A.n=0 | B.n=1 | C.n=2 | D.n≥3 |
若抛物线 的焦点与椭圆
的焦点与椭圆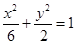 的左焦点重合,则
的左焦点重合,则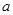 的值为( )
的值为( )
| A.-8 | B.-16 | C.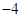 | D.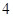 |
已知双曲线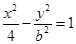 的右焦点与抛物线
的右焦点与抛物线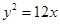 的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ).
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( ).
A.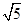 | B.4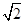 | C.3 | D.5 |
[2013·四川高考]抛物线y2=4x的焦点到双曲线x2- =1的渐近线的距离是( )
=1的渐近线的距离是( )
A.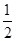 | B.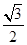 | C.1 | D.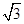 |
若双曲线 -
- =1(a>0,b>0)上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
=1(a>0,b>0)上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
A.(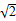 ,+∞) ,+∞) | B.[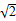 ,+∞) ,+∞) |
C.(1,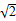 ] ] | D.(1,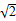 ) ) |
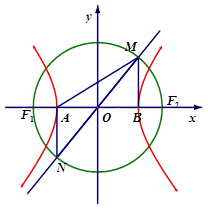
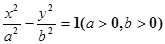 的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线的某条渐近线于M、N两点,且满足
的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线的某条渐近线于M、N两点,且满足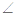 MAN=120o,则该双曲线的离心率为( )
MAN=120o,则该双曲线的离心率为( )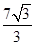
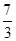
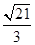
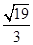
 轴上的双曲线
轴上的双曲线 的渐近线方程为
的渐近线方程为 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )


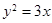 的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则
的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则