题目内容
【题目】已知数列{an}满足 ![]() 是等差数列,且b1=a1 , b4=a3 .
是等差数列,且b1=a1 , b4=a3 .
(1)求数列{an}和{bn}的通项公式;
(2)若 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】
(1)解:Sn=2an﹣1,n≥2时,Sn﹣1=2an﹣1﹣1,∴an=Sn﹣Sn﹣1=2an﹣2an﹣1,即an=2an﹣1.
当n=1时,S1=a1=2a1﹣1,∴a1=1,
∴an是以1为首项,2为公比的等比数列,
∴ ![]() ,
,
b1=a1=1,b4=a3=4,∴公差= ![]() =1.
=1.
bn=1+(n﹣1)=n
(2)解: ![]() ,
,
∴ 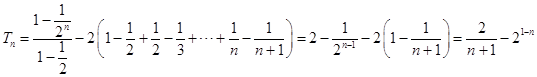
【解析】(1)利用递推关系、等差数列与等比数列的通项公式即可得出.(2)利用“裂项求和”方法、等比数列的求和公式即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系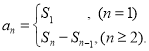 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100] |
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以上统计数据填写下面2×2列联表,并判断“成绩优良与教学方式是否有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]()
![]() . 临界值表
. 临界值表

【题目】![]() 是指空气中直径小于或等于
是指空气中直径小于或等于![]() 微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
微米的颗粒物(也称可入肺颗粒物).为了探究车流量与![]() 的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 |
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)根据上表数据,请在所给的坐标系中画出散点图;
(Ⅱ)根据上表数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)若周六同一时间段的车流量是![]() 万辆,试根据(Ⅱ)求出的线性回归方程,预测此时
万辆,试根据(Ⅱ)求出的线性回归方程,预测此时![]() 的浓度为多少(保留整数)?
的浓度为多少(保留整数)?
参考公式:由最小二乘法所得回归直线的方程是:![]() ,
,
其中 .
.