题目内容
【题目】如图1,已知四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() ,
, ![]() ,如图2,将
,如图2,将![]() ,
, ![]() 分别沿
分别沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,设
,设![]() 为
为![]() 上任意一点.
上任意一点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析(2)![]() 的值为
的值为![]() 或
或![]()
【解析】试题分析:(1)推导出CD⊥平面AED,CD⊥平面BCF,从而平面AED∥平面BCF,由此能证明DG∥平面BCF
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,设
,设![]() ,通过
,通过![]() 可得到
可得到![]() 值,在
值,在![]() 中求解可得到
中求解可得到![]() 的值
的值
试题解析:(1)由题意可知![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,设
,设![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴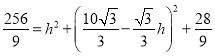 ,化简得
,化简得![]()
∴![]() 或
或![]() .
.
又∵![]() ,
,
当![]() 时,
时,
在![]() 中,
中, ![]() ,
,
∴![]() .
.
当![]() 时,同理可得
时,同理可得![]() ,
,
综上所述, ![]() 的值为
的值为![]() 或
或![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】一汽车![]() 店新进
店新进![]() 三类轿车,每类轿车的数量如下表:
三类轿车,每类轿车的数量如下表:
类别 |
|
|
|
数量 | 4 | 3 | 2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(1)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(2)若一次性提取4辆车,其中![]() 三种型号的车辆数分别记为
三种型号的车辆数分别记为![]() ,记
,记![]() 为
为![]() 的最大值,求
的最大值,求![]() 的分布列和数学期望.
的分布列和数学期望.
