题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的倾斜角为45°,以坐标原点为极点,
的倾斜角为45°,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 和曲线
和曲线![]() 的交点为点
的交点为点![]() .
.
(1)求直线![]() 的参数方程;
的参数方程;
(2)求![]() 的值.
的值.
【答案】(1) ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由于定点为![]() ,倾斜角为
,倾斜角为![]() ,根据直线参数方程的概念,有
,根据直线参数方程的概念,有 ;(2)对方程
;(2)对方程![]() 两边乘以
两边乘以![]() ,化简得
,化简得![]() ,将直线的参数方程代入,写出根与系数关系,理由难过参数的几何意义有
,将直线的参数方程代入,写出根与系数关系,理由难过参数的几何意义有![]() .
.
试题解析:
(1)由条件知,直线![]() 的倾斜角
的倾斜角![]() ,
,
设点![]() 是直线
是直线![]() 上的任意一点,点
上的任意一点,点![]() 到点
到点![]() 的有向距离为
的有向距离为![]() ,则
,则
 ....................5分
....................5分
(2)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,由此得
,由此得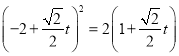 ,
,
即![]() ,设
,设![]() 为此方程的两个根,因为
为此方程的两个根,因为![]() 和
和![]() 的交点为
的交点为![]() ,所以
,所以![]() 分别是点
分别是点![]() 所对应的参数,由韦达定理得
所对应的参数,由韦达定理得![]() ................10分
................10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】一汽车![]() 店新进
店新进![]() 三类轿车,每类轿车的数量如下表:
三类轿车,每类轿车的数量如下表:
类别 |
|
|
|
数量 | 4 | 3 | 2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(1)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(2)若一次性提取4辆车,其中![]() 三种型号的车辆数分别记为
三种型号的车辆数分别记为![]() ,记
,记![]() 为
为![]() 的最大值,求
的最大值,求![]() 的分布列和数学期望.
的分布列和数学期望.
