题目内容
设定义在R上的函数f(x)=
,若关于x的方程f2(x)+bf(x)+c=0,有3个不等的实数根x1,x2,x3,则x1+x2+x3=( )
|
| A、0 | B、1 | C、3 | D、2 |
分析:作出f(x)的图象,根据函数图象的特点得到函数关于直线x=1对称.从而得出f2(x)+bf(x)+c=0必有一根使f(x)=1,利用数形结合即可得到结论.
解答:解:作出函数的图象如图: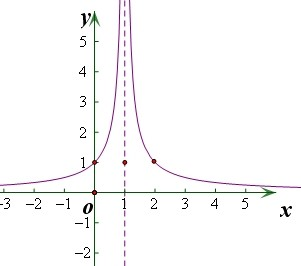
易知f(x)的图象关于直线x=1对称,
设t=f(x),
则当t=1时,方程f(x)=t有3个根,
当t>0且t≠1时,方程f(x)=t有2个根,
当t≤0时,方程f(x)=t有0个根,
对于方程f2(x)+bf(x)+c=0,是一个关于f(x)的一元二次方程,
若方程f2(x)+bf(x)+c=0,有3个不等的实数根x1,x2,x3,
则此一元二次方程仅有一根,即t=1,f(x)=1,
此时x1,x2,x3三个数中有一个是1,另两个关于x=1对称,此时有 x1+x2+x3=3,
故选:C.

易知f(x)的图象关于直线x=1对称,
设t=f(x),
则当t=1时,方程f(x)=t有3个根,
当t>0且t≠1时,方程f(x)=t有2个根,
当t≤0时,方程f(x)=t有0个根,
对于方程f2(x)+bf(x)+c=0,是一个关于f(x)的一元二次方程,
若方程f2(x)+bf(x)+c=0,有3个不等的实数根x1,x2,x3,
则此一元二次方程仅有一根,即t=1,f(x)=1,
此时x1,x2,x3三个数中有一个是1,另两个关于x=1对称,此时有 x1+x2+x3=3,
故选:C.
点评:本题主要考查方程根的个数的应用,利用数形结合是解决本题的关键,考查学生的综合应用能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |