题目内容
设定义在R上的函数f(x)满足f(x+π)=f(x-π),f(
-x)=f(
+x),当x∈[-
,
]时,0<f(x)<1;当x∈(-
,
)且x≠0时,x•f′(x)<0,则y=f(x)与y=cosx的图象在[-2π,2π]上的交点个数是( )
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
分析:确定函数f(x)的图象及性质,利用数形结合的方法,即可求得结论.
解答:解:∵f(x+π)=f(x-π),∴f(x+2π)=f(x),∴函数的周期为2π
∵f(
-x)=f(
+x),∴函数关于直线x=
对称
∵当x∈(-
,
)且x≠0时,x•f′(x)<0,
∴x∈[0,
)时,f(x)为单调减函数;x∈(-
,0)时,f(x)为单调增函数,
∵x∈[-
,
]时,0<f(x)<1,
∴y=f(x)与y=cosx的图象在[-2π,2π]上的图象如图所示
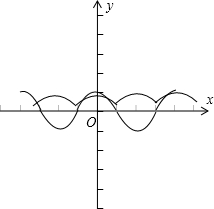
所以y=f(x)与y=cosx的图象在[-2π,2π]上的交点个数是4个
故选C.
∵f(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∵当x∈(-
| π |
| 2 |
| π |
| 2 |
∴x∈[0,
| π |
| 2 |
| π |
| 2 |
∵x∈[-
| π |
| 2 |
| π |
| 2 |
∴y=f(x)与y=cosx的图象在[-2π,2π]上的图象如图所示

所以y=f(x)与y=cosx的图象在[-2π,2π]上的交点个数是4个
故选C.
点评:本题考查函数与方程思想,考查数形结合,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设定义在R上的函数f(x)同时满足以下条件:①f(x+1)=-f(x)对任意的x都成立;②当x∈[0,1]时,f(x)=ex-e•cos
+m(其中e=2.71828…是自然对数的底数,m是常数).记f(x)在区间[2013,2016]上的零点个数为n,则( )
| πx |
| 2 |
A、m=-
| ||
| B、m=1-e,n=5 | ||
C、m=-
| ||
| D、m=e-1,n=4 |