题目内容
已知函数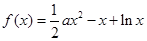 (
(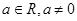 )
)
(1)当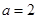 时,求曲线
时,求曲线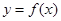 在
在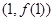 处的切线方程;
处的切线方程;
(2)若在区间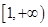 上函数
上函数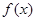 的图象恒在直线
的图象恒在直线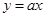 下方,求
下方,求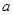 的取值范围.
的取值范围.
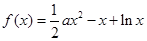 (
(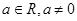 )
)(1)当
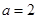 时,求曲线
时,求曲线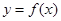 在
在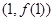 处的切线方程;
处的切线方程;(2)若在区间
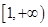 上函数
上函数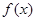 的图象恒在直线
的图象恒在直线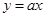 下方,求
下方,求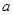 的取值范围.
的取值范围.(1) ;(2)
;(2)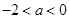
 ;(2)
;(2)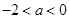
试题分析:(1)先求导函数
 ,由导数的几何意义知
,由导数的几何意义知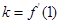 ,利用直线的点斜式方程求切线方程;(2)由题意,不等式
,利用直线的点斜式方程求切线方程;(2)由题意,不等式 恒成立,对于恒成立问题可考虑参变分离,也可以构造函数法,本题构造函数
恒成立,对于恒成立问题可考虑参变分离,也可以构造函数法,本题构造函数 ,等价于
,等价于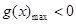 ,故利用导数求函数
,故利用导数求函数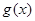 的最大值,求
的最大值,求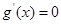 的根,得
的根,得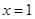 或
或 ,讨论根的大小并和定义域比较,同时要注意分子二次函数的开口方向,通过判断函数大致图像,从而求函数的最大值,进而列不等式求
,讨论根的大小并和定义域比较,同时要注意分子二次函数的开口方向,通过判断函数大致图像,从而求函数的最大值,进而列不等式求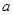 的取值范围.
的取值范围.试题解析:(1)函数的定义域为
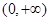 .
.当
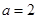 时,
时,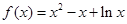 ,
, ,则
,则 ,又切点为
,又切点为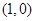 ,故曲线
,故曲线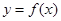 在
在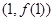 处的切线方程为
处的切线方程为 .
.(2)令
 定义域
定义域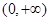
在区间
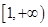 上,函数
上,函数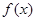 的图象恒在直线
的图象恒在直线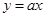 下方,等价于
下方,等价于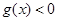 在
在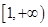 恒成立,即
恒成立,即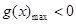 ,
,
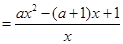
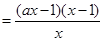 ,令
,令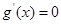 ,得
,得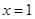 或
或 ,
,当
 时,
时, ,故
,故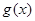 在
在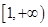 单调递减,则
单调递减,则 ,得
,得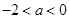 ;
;当
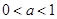 时,
时,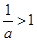 ,当
,当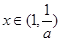 时,
时, ,
,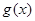 单调递减;当
单调递减;当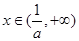 时,
时,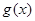 单调递增,此时
单调递增,此时 ,故不可能
,故不可能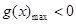 ,不合题意;
,不合题意;当
 时,
时,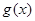 在
在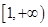 单调递增,
单调递增, ,故不可能
,故不可能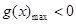 ,不合题意.
,不合题意.综上:
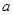 的取值范围
的取值范围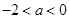 .
.
练习册系列答案
相关题目
 的最大值为( )
的最大值为( )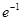
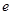
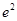

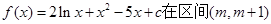 上为递减函数,则m的取值范围是 。
上为递减函数,则m的取值范围是 。 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .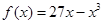 在区间
在区间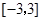 上的最小值是_________________;
上的最小值是_________________;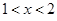 ,则
,则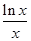 、
、 、
、 的大小关系是( )
的大小关系是( )
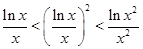

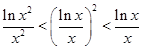
 是
是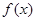 的导函数,
的导函数,
 在R上可导,其导函数
在R上可导,其导函数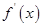 ,且函数
,且函数 处取得极小值,则函数
处取得极小值,则函数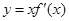 的图像可能是( )
的图像可能是( )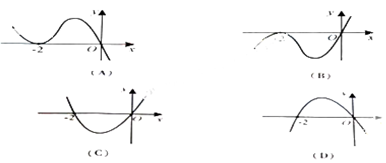
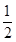 x2+blnx在区间[
x2+blnx在区间[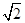 ,+∞)上是减函数,则b的取值范围是________.
,+∞)上是减函数,则b的取值范围是________.