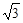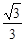题目内容
(本题14分)向量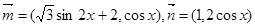 ,设函数
,设函数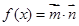 .
.
(1)求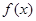 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在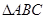 中,
中,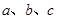 分别是角
分别是角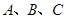 的对边,若
的对边,若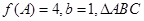 的面积
的面积
为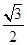 ,求a的值.
,求a的值.
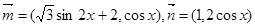 ,设函数
,设函数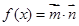 .
.(1)求
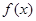 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;(2)在
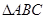 中,
中,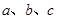 分别是角
分别是角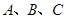 的对边,若
的对边,若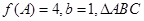 的面积
的面积为
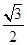 ,求a的值.
,求a的值. (1) ,
,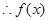 的单调递减区间为
的单调递减区间为 ,k∈Z;
,k∈Z;
(2) 。
。
 ,
,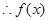 的单调递减区间为
的单调递减区间为 ,k∈Z;
,k∈Z;(2)
 。
。(1)先根据数量积的坐标表示可得
 ,再根据三角恒等变换公式可得
,再根据三角恒等变换公式可得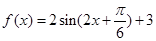 ,所以
,所以 ,再由正弦函数的单调递减区间求出f(x)的递减区间.
,再由正弦函数的单调递减区间求出f(x)的递减区间.
(2)由f(A)=4可得求出A,然后根据面积公式 求出c值.在三角形ABC中,已知b,c及A,显然再利用余弦定理求a即可.
求出c值.在三角形ABC中,已知b,c及A,显然再利用余弦定理求a即可.
(1) ,
,


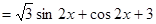
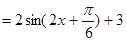 ……4分
……4分  ………5分
………5分
令

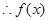 的单调递减区间为
的单调递减区间为 ,k∈Z………………………………7分
,k∈Z………………………………7分
(2)由 得
得 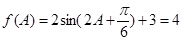
 …………8分
…………8分
又 为
为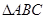 的内角,
的内角, ,
,
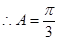 …10分
…10分
 ,
, ,
,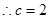 ……………………………12分
……………………………12分
 ,
, …………………14分
…………………14分

 ,再根据三角恒等变换公式可得
,再根据三角恒等变换公式可得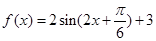 ,所以
,所以 ,再由正弦函数的单调递减区间求出f(x)的递减区间.
,再由正弦函数的单调递减区间求出f(x)的递减区间.(2)由f(A)=4可得求出A,然后根据面积公式
 求出c值.在三角形ABC中,已知b,c及A,显然再利用余弦定理求a即可.
求出c值.在三角形ABC中,已知b,c及A,显然再利用余弦定理求a即可.(1)
 ,
,

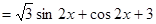
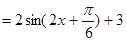 ……4分
……4分  ………5分
………5分令


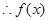 的单调递减区间为
的单调递减区间为 ,k∈Z………………………………7分
,k∈Z………………………………7分(2)由
 得
得 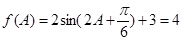
 …………8分
…………8分又
 为
为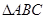 的内角,
的内角, ,
,
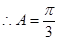 …10分
…10分 ,
, ,
,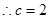 ……………………………12分
……………………………12分 ,
, …………………14分
…………………14分 
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 )的部分图象.
)的部分图象. =
= ,0<α<
,0<α< ,求cosα的值.
,求cosα的值.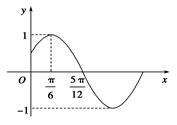
 ,则
,则 ( )
( )



 ,函数
,函数 ,
, 时,
时, ,求常数
,求常数 ,
,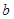 的值.
的值. 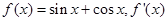 是
是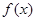 的导函数.
的导函数.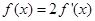 ,求
,求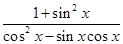 的值.
的值. 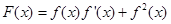 (
(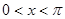 )的单调增区间。
)的单调增区间。  ,其中a、b、c分别是
,其中a、b、c分别是 的三内角A、B、C的对边长.
的三内角A、B、C的对边长. 的值;
的值; 的最大值.
的最大值. 的一部分图象如图,那么
的一部分图象如图,那么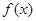 的解析式以及
的解析式以及
 的值分别是( )
的值分别是( )
 ,
, 
 ,
, 
 ,
,  ,
,  (
( )的图象如右图所示,为了得到
)的图象如右图所示,为了得到 的图象,可以将
的图象,可以将 的图象( )
的图象( )
 个单位长度
个单位长度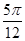 个单位长度
个单位长度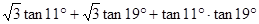 的值是( ).
的值是( ).