题目内容
2.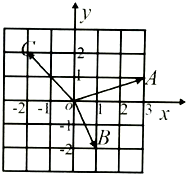 如图,在复平面内,已知复数z1、z2、z3,对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,(i是虚数单位),已知z=$\frac{{z}_{1}•{z}_{2}}{{z}_{3}}$则|$\overrightarrow{z}$+$\frac{\sqrt{11}}{2}$i|=( )
如图,在复平面内,已知复数z1、z2、z3,对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,(i是虚数单位),已知z=$\frac{{z}_{1}•{z}_{2}}{{z}_{3}}$则|$\overrightarrow{z}$+$\frac{\sqrt{11}}{2}$i|=( )| A. | 3 | B. | $\sqrt{10+\sqrt{11}}$ | C. | $\sqrt{6+\sqrt{11}}$ | D. | $\frac{3}{2}$ |
分析 求出复数z1、z2、z3,然后利用复数的乘除运算法则求解z,再求解复数的模.
解答 解:由题意可知复数z1=3+i,
z2=1-2i,
z3=-2+2i,
∴$z=\frac{{z}_{1}•{z}_{2}}{{z}_{3}}$=$\frac{(3+i)(1-2i)}{-2+2i}$=$\frac{5-5i}{-2+2i}$=$-\frac{5}{2}$,
$|\overline{z}+\frac{\sqrt{11}}{2}i|$=$|-\frac{5}{2}+\frac{\sqrt{11}}{2}i|$=$\sqrt{(-\frac{5}{2})^{2}+(\frac{\sqrt{11}}{2})^{2}}$=3.
故选:A.
点评 本题考查了复数的几何意义和复数的模的计算公式,属于基础题.

练习册系列答案
相关题目
10.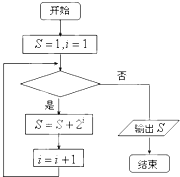 阅读右边的程序框图,为使输出的数据为127,则判断框中应填入的条件为( )
阅读右边的程序框图,为使输出的数据为127,则判断框中应填入的条件为( )
 阅读右边的程序框图,为使输出的数据为127,则判断框中应填入的条件为( )
阅读右边的程序框图,为使输出的数据为127,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
7.设函数f(x)=$\left\{\begin{array}{l}{|lnx|,x>0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$,若f(a)+f(-1)=3,则a=( )
| A. | e | B. | $\frac{1}{e}$ | C. | e或$\frac{1}{e}$ | D. | 1 |
11.设a>0,b>0,若点P(1,1)到直线(a+1)x+(b+1)y-2=0的距离为1,则ab的取值范围是( )( )
| A. | $[{\sqrt{2}-1,+∞})$ | B. | $[{3-2\sqrt{2},+∞})$ | C. | $[{1+\sqrt{2},+∞})$ | D. | $[{3+2\sqrt{2},+∞})$ |
12.已知点A(1,$\sqrt{3}$),B(-1,-$\sqrt{3}$),则直线AB的倾斜角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
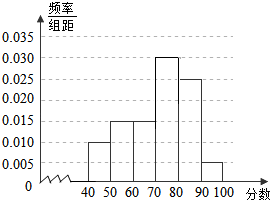 某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.