题目内容
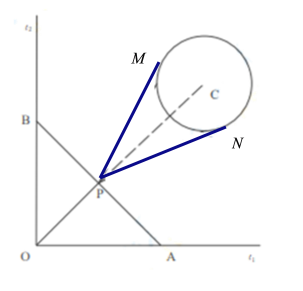
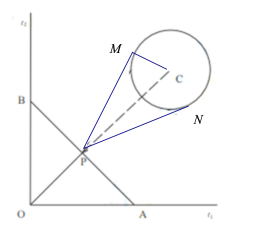
【题目】如图，在一旅游区内原有两条互相垂直且相交于点O的道路l1，l2，一自然景观的边界近似为圆形，其半径约为1千米，景观的中心C到l1，l2的距离相等，点C到点O的距离约为10千米.现拟新建四条游览道路方便游客参观，具体方案：在线段OC上取一点P，新建一条道路OP，并过点P新建两条与圆C相切的道路PM，PN（M，N为切点），同时过点P新建一条与OP垂直的道路AB（A，B分别在l1，l2上）.为促进沿途旅游经济，新建道路长度之和越大越好，求新建道路长度之和的最大值.（所有道路宽度忽略不计）
【答案】
千米
【解析】
设PCM＝，用
表示出各道路长，并求出和
.然后求导，用导数知识求得最大值．
解：连接CM，设PCM＝，则PC＝
，PM＝PN＝tan，
OP＝OC﹣PC＝10﹣，AB＝2OP＝20﹣
，
设新建的道路长度之和为，
则
，
由1＜PC≤10得
≤
＜1，设
，
(0，
)，
则
(0，
]，
，
，令
得
设
，
(0，]，，
，
的情况如下表：
| (0， |
| ( |
| ＋ | 0 | － |
| 单调递增 | 极大值 | 单调递减 |
由表可知
时有极大值也是最大值，此时，
，
，
.
答：新建道路长度之和的最大值为千米.
练习册系列答案
相关题目
