题目内容
(本小题满分8分)A、B两城相距100km,在两地之间距A城xkm处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数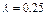 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.
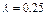 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.
(Ⅰ)y=5x2+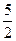 (100—x)2(10≤x≤90);(Ⅱ)当核电站建在距A城
(100—x)2(10≤x≤90);(Ⅱ)当核电站建在距A城 米时,才能使供电费用最小
米时,才能使供电费用最小
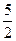 (100—x)2(10≤x≤90);(Ⅱ)当核电站建在距A城
(100—x)2(10≤x≤90);(Ⅱ)当核电站建在距A城 米时,才能使供电费用最小
米时,才能使供电费用最小解:(Ⅰ)y=5x2+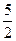 (100—x)2(10≤x≤90);…………………………5分
(100—x)2(10≤x≤90);…………………………5分
(Ⅱ)由y=5x2+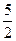 (100—x)2=
(100—x)2= x2-500x+25000=
x2-500x+25000=
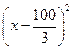 +
+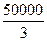 .
.
则当x= 米时,y最小.
米时,y最小.
故当核电站建在距A城 米时,才能使供电费用最小.……………………………8分
米时,才能使供电费用最小.……………………………8分
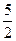 (100—x)2(10≤x≤90);…………………………5分
(100—x)2(10≤x≤90);…………………………5分(Ⅱ)由y=5x2+
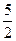 (100—x)2=
(100—x)2= x2-500x+25000=
x2-500x+25000=
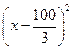 +
+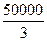 .
.则当x=
 米时,y最小.
米时,y最小.故当核电站建在距A城
 米时,才能使供电费用最小.……………………………8分
米时,才能使供电费用最小.……………………………8分
练习册系列答案
相关题目
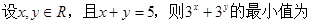 ( )
( )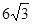
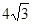
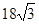
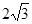
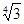
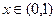 则
则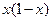 的最大值为 ▲
的最大值为 ▲ 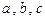 满足
满足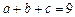 ,
,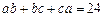 ,则
,则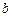 的取值范围是 ▲ .
的取值范围是 ▲ .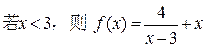 的最大值是
的最大值是 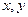 满足
满足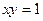 ,则
,则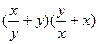 的最小
的最小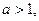 则
则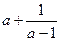 的最小值是________
的最小值是________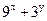 的最小值为
的最小值为