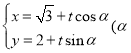题目内容
【题目】为了调查居民对城市共享单车的满意度,随机选取了100人进行问卷调查,并将问卷中的100人根据其满意度评分值按照![]() 分为5组,得到号如图所示的频率分布直方图.
分为5组,得到号如图所示的频率分布直方图.
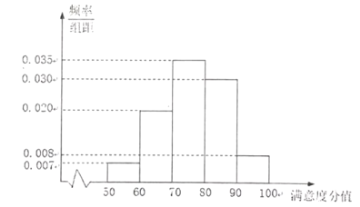
(Ⅰ)求满意度分值不低于70分的人数.
(Ⅱ)已知满意度分值在![]() 内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在
内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在![]() 的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
【答案】(Ⅰ)73人(Ⅱ)![]()
【解析】
(I)计算出![]() 分以上的频率,然后乘以
分以上的频率,然后乘以![]() 得到所求的人数.(II)先求得
得到所求的人数.(II)先求得![]() 内的人数为
内的人数为![]() 人,其中男性
人,其中男性![]() 人,女性
人,女性![]() 人,利用列举法和古典概型概率计算公式计算出所求的概率.
人,利用列举法和古典概型概率计算公式计算出所求的概率.
解:(Ⅰ)由频率分布直方图可知满意度分值不低于70分的人数为:
![]() (人),
(人),
∴满意度分值不低于70分的人数为73人.
(Ⅱ)![]() 的样本内共有居民
的样本内共有居民![]() 人,3名男性,4名女性,
人,3名男性,4名女性,
设三名男性分别表示为![]() ,四名女性分别表示为
,四名女性分别表示为![]()
则从7名居民随机抽取2名的所有可能结果为:
![]()
![]()
![]()
![]()
![]()
![]() ,共21种.
,共21种.
设事件![]() 为“抽取2人中只有一位男性”,则
为“抽取2人中只有一位男性”,则![]() 中所含的结果为:
中所含的结果为:
![]()
![]()
![]()
共12种
∴事件![]() 发生的概率为
发生的概率为![]() .
.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目