题目内容
(本小题满分16分)已知函数f(x)=x2-(1+2a)x+alnx(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
解:(1)当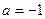 时,
时,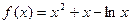 则
则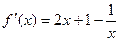
所以 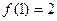 ,且
,且 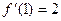 .
.
所以曲线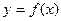 在
在 处的切线的方程为:
处的切线的方程为: ,
,
即: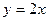 .
.
(2).由题意得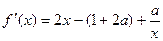 =
=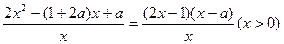
由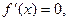 得
得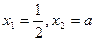
①当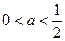 时,由
时,由 ,又知
,又知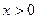 得
得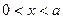 或
或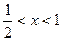
由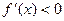 ,又知
,又知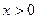 ,得
,得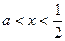
所以函数 的单调增区间是
的单调增区间是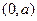 和
和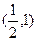 ,单调减区间是
,单调减区间是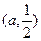
②当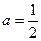 时,
时,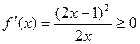 ,且仅当
,且仅当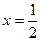 时,
时,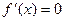 ,
,
所以函数 在区间
在区间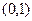 上是单调增函数.
上是单调增函数.
③当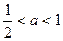 时, 由
时, 由 ,又知
,又知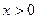 得
得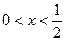 或
或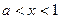
由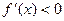 ,又知
,又知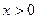 ,得
,得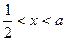
所以函数 的单调增区间是
的单调增区间是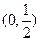 和
和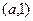 ,单调减区间是
,单调减区间是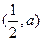
④当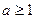 时, 由
时, 由 ,又知
,又知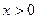 得
得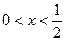
由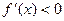 ,又知
,又知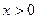 ,得
,得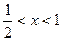
所以函数 的单调增区间是
的单调增区间是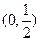 ,单调减区间是
,单调减区间是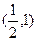
解析

练习册系列答案
相关题目
设 ,
, ,则从
,则从 到
到 的映射有( )
的映射有( )
| A.7个 | B.8个 | C.9个 | D.10个 |
 .
.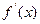 的解析式;
的解析式; ,讨论函数
,讨论函数 的单调性;
的单调性; ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 过点
过点 ,且与曲线
,且与曲线 和
和 都相切,
都相切, 的值。
的值。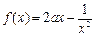 ,
, .
.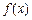 在
在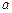 的取值范围;
的取值范围;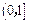 上的最大值.
上的最大值. 某厂家拟在2012年举行促销活动,经调查测算,该产品的
某厂家拟在2012年举行促销活动,经调查测算,该产品的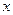 万件与年促销费用
万件与年促销费用 万元(
万元( (
( 为
为 两部分资金).
两部分资金). 润最大?
润最大?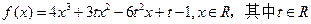 ,
,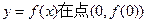 处的切线方程;
处的切线方程;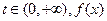 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。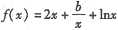 的一个极值点
的一个极值点 ,试问过点(2,5)可作多少条直线与曲线
,试问过点(2,5)可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由. 的图象过点(1, -4),且函数
的图象过点(1, -4),且函数 的图象关于y轴对称.
的图象关于y轴对称. 的极值;
的极值; 在区间
在区间 上的最大值。
上的最大值。