题目内容
【题目】已知函数f(x)=f'(1)ex﹣1﹣f(0)x+ ![]() 的导数,e为自然对数的底数)g(x)=
的导数,e为自然对数的底数)g(x)= ![]() +ax+b(a∈R,b∈R)
+ax+b(a∈R,b∈R)
(Ⅰ)求f(x)的解析式及极值;
(Ⅱ)若f(x)≥g(x),求 ![]() 的最大值.
的最大值.
【答案】解:(Ⅰ)由已知得:f′(x)=f′(1)ex﹣1﹣f(0)+x,令x=1,得:f′(1)=f′(1)﹣f(0)+1,
即f(0)=1,
∵f(0)= ![]() ,
,
∴f′(1)=e,
从而f(x)=ex﹣x+ ![]() x2 ,
x2 ,
∴f′(x)=ex+x﹣1,
又f′(x)=ex+x﹣1在R递增,且f′(0)=0,
∴当x<0时,f′(x)<0,x>0时,f′(x)>0,
故x=0为极值点,
∴f(0)= ![]() ;
;
(Ⅱ)f(x)≥ ![]() x2+ax+bh(x)=ex﹣(a+1)x﹣b≥0,
x2+ax+bh(x)=ex﹣(a+1)x﹣b≥0,
得:h′(x)=ex﹣(a+1),
①当a+1≤0时,h′(x)>0,
故y=h(x)在x∈R上递增,
x∈﹣∞时,h(x)→﹣∞与h(x)≥0矛盾,
②当a+1>0时,h′(x)>0,
∴x>ln(a+1),h′(x)<0,
∴x<ln(a+1),
故x=ln(a+1)时,h(x)min=(a+1)﹣(a+1)ln(a+1)﹣b≥0,
即(a+1)﹣(a+1)ln(a+1)≥b,
∴(a+1)b≤(a+1)2﹣(a+1)2ln(a+1),(a+1>0),
令F(x)=x3﹣x2lnx(x>0),则F′(x)=x(1﹣2lnx),
∴F′(x)>0,解得:0<x< ![]() ,F′(x)<0,解得:x>
,F′(x)<0,解得:x> ![]() ,
,
x= ![]() 时,F(x)max=
时,F(x)max= ![]() ,
,
即当a= ![]() ﹣1,b=
﹣1,b= ![]() 时,
时,
(a+1)b的最大值为 ![]() ,
,
∴ ![]() 的最大值为:
的最大值为: ![]()
【解析】(Ⅰ)求出函数的导数,求出f′(1)=e,求出函数的导数,得到函数的单调性求出f(0)的值即可;(Ⅱ)令h(x)=ex﹣(a+1)x﹣b≥0,求出函数的导数,通过讨论a的范围,求出函数的单调区间,求出 ![]() 的最大值即可.
的最大值即可.
【考点精析】通过灵活运用基本求导法则和函数的极值与导数,掌握若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧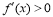 ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.