Question

【题目】如图，定义在[﹣2，2]的偶函数f（x）的图象如图所示，则方程f（f（x））=0的实根个数为（ ）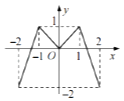
A.3
B.4
C.5
D.7

Answer 1

【答案】C
【解析】解：定义在[﹣2，2]的偶函数f（x）的图象如图：

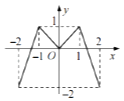
函数是偶函数，

函数的值域为：f（x）∈[﹣2，1]，函数的零点为：x1，0，x2，

x1∈（﹣2，﹣1），x2∈（1，2），

令t=f（x），则f（f（x））=0，即f（t）=0可得，t=x1，0，x2，

f（x）=x1∈（﹣2，﹣1）时，存在f[f（x1）]=0，

此时方程的根有2个．

x2∈（1，2）时，不存在f[f（x2）]=0，方根程没有根．

f[f（0）]=f（0）=f（x1）=f（x2）=0，有3个．

所以方程f（f（x））=0的实根个数为：5个．

故选：C．