题目内容
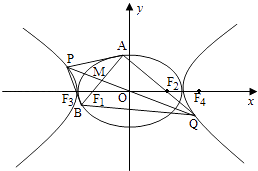
【题目】已知点![]() ,
,![]() 分别为线段
分别为线段![]() 上的动点,且满足
上的动点,且满足![]()
(1)若![]() 求直线
求直线![]() 的方程;
的方程;
(2)证明:![]() 的外接圆恒过定点(异于原点)。
的外接圆恒过定点(异于原点)。
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
试题(1)求直线CD的方程,只需确定C,D坐标即可:![]() ,
,![]() ,直线
,直线![]() 的斜率
的斜率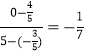 ,直线
,直线![]() 的方程为
的方程为![]() .
.
(2)证明动圆过定点,关键在于表示出圆的方程,本题适宜设圆的一般式:![]() 设
设![]() ,则D
,则D![]() ,从而
,从而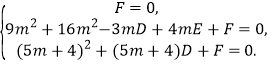 解之得
解之得![]() ,
,![]() ,整理得
,整理得![]() ,所以△
,所以△![]() 的外接圆恒过定点为
的外接圆恒过定点为![]() .
.
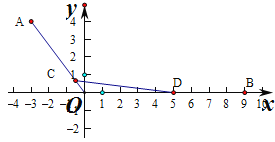
试题解析:(1)因为![]() ,所以
,所以![]() , 1分
, 1分
又因为![]() ,所以
,所以![]() ,所以
,所以![]() , 3分
, 3分
由![]() ,得
,得![]() , 4分
, 4分
所以直线![]() 的斜率
的斜率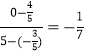 , 5分
, 5分
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() . 6分
. 6分
(2)设![]() ,则
,则![]() . 7分
. 7分
则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 点的坐标为
点的坐标为![]() 8分
8分
又设![]() 的外接圆的方程为
的外接圆的方程为![]() ,
,
则有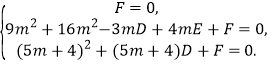 10分
10分
解之得![]() ,
,![]() ,
,
所以![]() 的外接圆的方程为
的外接圆的方程为![]() , 12分
, 12分
整理得![]() ,
,
令![]() ,所以
,所以![]() (舍)或
(舍)或![]()
所以△![]() 的外接圆恒过定点为
的外接圆恒过定点为![]() . 14分
. 14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目