题目内容
20.若集合A={x|x>3},B={x|1<x<4},则A∩B=( )| A. | ∅ | B. | {x|3<x<4} | C. | {x|-2<x<1} | D. | {x|x>4} |
分析 由A与B,求出两集合的交集即可.
解答 解:∵A={x|x>3},B={x|1<x<4},
∴A∩B={x|3<x<4},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
15.2≤|x|+|y|≤3,则x2+y2-2x的取值范围是( )
| A. | [$\frac{\sqrt{2}-2}{2}$,3] | B. | [$\frac{\sqrt{2}}{2}$,4] | C. | [-$\frac{1}{2}$,15] | D. | [$\frac{1}{2}$,16] |
9.设集合M={-1,0,1},N={x|x2-2x=0},则M∩N=( )
| A. | {-1,0,1} | B. | {0,1} | C. | {1} | D. | {0} |
10.已知命题p:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1上一点P到左焦点距离为8,则P到右焦点距离为2或14;命题q:椭圆离心率越大,椭圆越趋近于圆.则下列命题中为真命题的是( )
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨(¬q) |
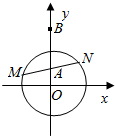 己知圆O:x2十y2=l,及A(0,$\sqrt{2}$-l),B(0,$\sqrt{2}$+l):
己知圆O:x2十y2=l,及A(0,$\sqrt{2}$-l),B(0,$\sqrt{2}$+l):