题目内容
10.已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=-12y的焦点.(1)求椭圆C的方程;
(2)过点M(m,0)的直线l与椭圆C相切(m<-2$\sqrt{3}$),直线l与y轴交于点N,当m为何值时△OMN的面积有最小值?并求出最小值.
分析 (1)通过抛物线x2=-12y可知b=3,再利用$e=\frac{c}{a}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{1}{2}$知a2=12,从而可得结论;
(2)设直线l的方程为y=k(x-m),联立直线l与椭圆方程,通过直线l与椭圆C相切得${m}^{2}=\frac{9}{{k}^{2}}+12$,从而N(0,-km),利用基本不等式可得S△OMN≥$6\sqrt{3}$.
解答 解:(1)由抛物线x2=-12y可知,其焦点为(0,-3),即b=3,
又$e=\frac{c}{a}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}=\frac{1}{2}$,∴a2=12,
∴椭圆C的方程为$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$;
(2)设直线l的方程为y=k(x-m),由对称性不妨设k>0,
联立直线l与椭圆方程,消去y得:(3+4k2)x2-8k2mx+4k2m2-36=0,
∵直线l与椭圆C相切,∴△=64k4m2-4(3+4k2)(4k2m2-36)=0,
化简,得${m}^{2}=\frac{9}{{k}^{2}}+12$,
令y=k(x-m)中x=0,得y=-km,即N(0,-km),
∴S△OMN=$\frac{1}{2}(-m)(-km)$=$\frac{1}{2}k{m}^{2}$=$\frac{1}{2}k(\frac{9}{{k}^{2}}+12)$,
∴S△OMN=$\frac{1}{2}(\frac{9}{k}+12k)$≥$\sqrt{\frac{9}{k}×12k}$=$6\sqrt{3}$
当且仅当$\frac{9}{k}=12k$即$k=\frac{\sqrt{3}}{2}$时等号成立,
∵m<-2$\sqrt{3}$,∴$m=-2\sqrt{6}$时,S△OMN有最小值$6\sqrt{3}$.
点评 本题考查椭圆的简单性质,抛物线的简单性质,直线与椭圆的位置关系,基本不等式,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 若m⊥n,则α⊥β | B. | 若m∥n,则α⊥β | C. | 若m⊥n,则α∥β | D. | 若m∥n,则α∥β |

 如图,在多面体ABCDEF中,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点,N为CD的中点.
如图,在多面体ABCDEF中,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点,N为CD的中点.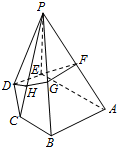 如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.
如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.