题目内容
(本小题满分12分)已知函数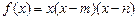 .
.
(I)当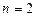 时,若函数
时,若函数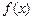 在
在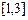 上单调递减,求实数
上单调递减,求实数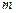 的取值范围;
的取值范围;
(II)若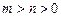 ,
,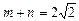 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线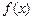 均相切,求
均相切,求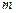 和
和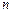 的值.
的值.
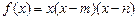 .
.(I)当
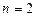 时,若函数
时,若函数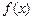 在
在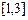 上单调递减,求实数
上单调递减,求实数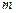 的取值范围;
的取值范围;(II)若
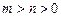 ,
,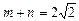 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线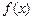 均相切,求
均相切,求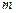 和
和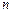 的值.
的值.(本小题满分12分)
解:(I)当 时,
时,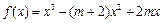 ,则
,则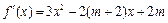 ,…(2分)
,…(2分)
函数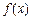 在
在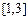 上单调递减,则有:
上单调递减,则有: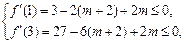
解得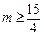 ,故实数m的取值范围是
,故实数m的取值范围是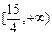 ; ………………(6分)
; ………………(6分)
(II)设切点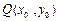 ,
,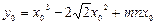
则切线的斜率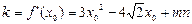 ,所以切线的方程是
,所以切线的方程是
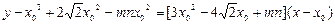 ,……………(8分)
,……………(8分)
又切线过原点,则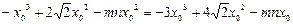 ,
,
∴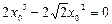 ,解得
,解得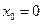 ,或
,或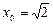 .
.
两条切线的斜率为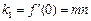 ,
,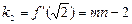
∵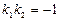 ,∴
,∴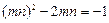 ,∴
,∴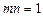 ,
,
由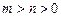 ,
,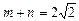 得
得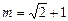 ,
,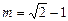 .………………(12分)
.………………(12分)
解:(I)当
 时,
时,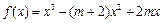 ,则
,则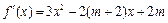 ,…(2分)
,…(2分)函数
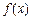 在
在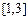 上单调递减,则有:
上单调递减,则有: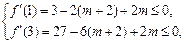
解得
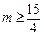 ,故实数m的取值范围是
,故实数m的取值范围是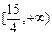 ; ………………(6分)
; ………………(6分)(II)设切点
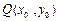 ,
,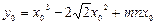
则切线的斜率
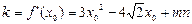 ,所以切线的方程是
,所以切线的方程是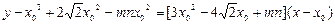 ,……………(8分)
,……………(8分)又切线过原点,则
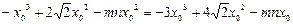 ,
,∴
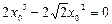 ,解得
,解得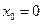 ,或
,或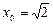 .
.两条切线的斜率为
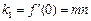 ,
,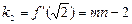
∵
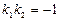 ,∴
,∴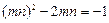 ,∴
,∴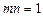 ,
,由
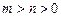 ,
,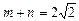 得
得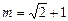 ,
,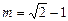 .………………(12分)
.………………(12分)略

练习册系列答案
相关题目
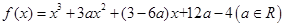

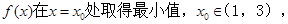 求a的取值范围.
求a的取值范围.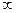 )上的函数
)上的函数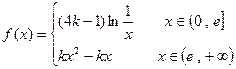 是增函数
是增函数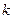 的取值范围
的取值范围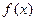 (
(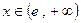 )的图象有交点,求该直线的斜率的取值范围
)的图象有交点,求该直线的斜率的取值范围 ,则
,则 等于
等于 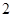


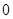
 )已知函数
)已知函数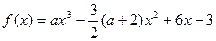 (a为常数)
(a为常数)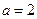 时,分析函数
时,分析函数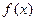 的单调性;
的单调性;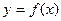 与
与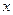 轴的公共点的个数。
轴的公共点的个数。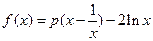 ,
,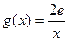 ,
,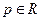 ,
,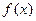 在
在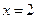 处取得极值,求
处取得极值,求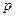 的值;
的值;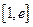 上至少存在一点
上至少存在一点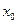 ,使得
,使得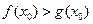 成立,求
成立,求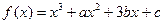 ,
,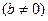 且
且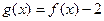 为奇函数.
为奇函数.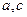 的值.
的值.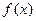 的单调区间
的单调区间 =
= 的图象与直线12x+y-1=0相切于点(1,-11),则a+b的值为( )
的图象与直线12x+y-1=0相切于点(1,-11),则a+b的值为( )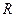 上的函数
上的函数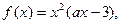 其中
其中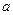 为常数。
为常数。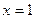 是函数
是函数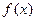 的一个极值点,求
的一个极值点,求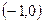 上为增函数,求
上为增函数,求