题目内容
设直线l的斜率为2且过抛物线y2=ax(a≠0)的焦点F,又与y轴交于点A,O为坐标原点,若△OAF的面积为4,则抛物线的方程为( )A.y2=4
B.y2=8
C.y2=±4
D.y2=±8
【答案】分析:先根据抛物线方程表示出F的坐标,进而根据点斜式表示出直线l的方程,求得A的坐标,进而利用三角形面积公式表示出三角形的面积建立等式取得a,则抛物线的方程可得.
解答:解:抛物线y2=ax(a≠0)的焦点F坐标为( ,0),
,0),
则直线l的方程为y=2(x-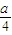 ),
),
它与y轴的交点为A(0,- ),
),
所以△OAF的面积为 |
| |•|
|•| |=4,
|=4,
解得a=±8.
所以抛物线方程为y2=±8x,
故选D.
点评:本题主要考查了抛物线的标准方程,点斜式求直线方程等.考查学生的数形结合的思想的运用和基础知识的灵活运用.
解答:解:抛物线y2=ax(a≠0)的焦点F坐标为(
 ,0),
,0),则直线l的方程为y=2(x-
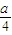 ),
),它与y轴的交点为A(0,-
 ),
),所以△OAF的面积为
 |
| |•|
|•| |=4,
|=4,解得a=±8.
所以抛物线方程为y2=±8x,
故选D.
点评:本题主要考查了抛物线的标准方程,点斜式求直线方程等.考查学生的数形结合的思想的运用和基础知识的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目