题目内容
已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
(1)若|AF|=4,求点A的坐标;
(2)设直线l的斜率为k,当线段AB的长等于5时,求k的值.
(3)求抛物线y2=4x上一点P到直线2x-y+4=0的距离的最小值.并求此时点P的坐标.
(1)若|AF|=4,求点A的坐标;
(2)设直线l的斜率为k,当线段AB的长等于5时,求k的值.
(3)求抛物线y2=4x上一点P到直线2x-y+4=0的距离的最小值.并求此时点P的坐标.
分析:(1)设A(x1,y1),则|AF|=x1+
,求出x1,代入y2=4x,即可求点A的坐标;
(2)直线l的方程为y=k(x-1),与抛物线方程联立,利用|AB|=x1+x2+p=5,即可求k的值.
(3)设P(x,y),求出P到直线2x-y+4=0的距离,利用配方法求最值.
| p |
| 2 |
(2)直线l的方程为y=k(x-1),与抛物线方程联立,利用|AB|=x1+x2+p=5,即可求k的值.
(3)设P(x,y),求出P到直线2x-y+4=0的距离,利用配方法求最值.
解答:解:由y2=4x,得p=2,其准线方程为x=-1,焦点F(1,0).设A(x1,y1),B(x2,y2).
(1)|AF|=x1+
,从而x1=4-1=3.代入y2=4x,得y=±2
.
所以点A为(3,2
)或(3,-2
)
(2)直线l的方程为y=k(x-1),与抛物线方程联立,消去y,整理得k2x2-(2k2+4)x+k2=0(*),
因为直线与抛物线相交于A、B两点,则k≠0,
设其两根为x1,x2,则x1+x2=2+
.
由抛物线的定义可知,|AB|=x1+x2+p=4+
=5,解得k=±2;
(3)设P(x,y),则P到直线2x-y+4=0距离为d=
=
=
∴y=1时,P到直线2x-y+4=0距离的最小值为
,此时P(0.25,1).
(1)|AF|=x1+
| p |
| 2 |
| 3 |
所以点A为(3,2
| 3 |
| 3 |
(2)直线l的方程为y=k(x-1),与抛物线方程联立,消去y,整理得k2x2-(2k2+4)x+k2=0(*),
因为直线与抛物线相交于A、B两点,则k≠0,
设其两根为x1,x2,则x1+x2=2+
| 4 |
| k2 |
由抛物线的定义可知,|AB|=x1+x2+p=4+
| 4 |
| k2 |
(3)设P(x,y),则P到直线2x-y+4=0距离为d=
| |2x-y+4| | ||
|
|
| ||
|
|
| ||||
|
∴y=1时,P到直线2x-y+4=0距离的最小值为
7
| ||
| 10 |
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查点到直线的距离的运用,考查配方法,正确运用点到直线的距离公式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
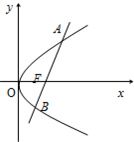 已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.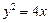 的焦点F,
的焦点F,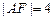 ,求点A的坐标;
,求点A的坐标;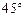 ,求线段AB的长.
,求线段AB的长.
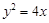 的焦点F,
的焦点F,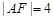 ,求点A的坐标;
,求点A的坐标;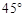 ,求线段AB的长.
,求线段AB的长.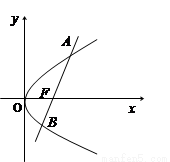
 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.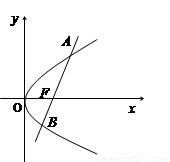
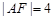 ,求点A的坐标;
,求点A的坐标;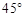 ,求线段AB的长.
,求线段AB的长.