Question

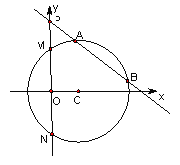
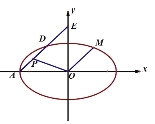
【题目】如图，在平面直角坐标系中，已知椭圆：的离心率，左顶点为，过点作斜率为的直线交椭圆于点，交轴于点.

（1）求椭圆的方程;

（2）已知为的中点，存在定点，使得对于任意的都有，求点的坐标;

（3）若过点作直线的平行线交椭圆于点，求的最小值.

Answer 1

【答案】（1）（2）（3）

【解析】

试题分析：（1）由椭圆的离心率和左顶点，求出a，b，由此能求出椭圆C的标准方程．（2）直线l的方程为y=k（x+4），与椭圆联立，得，（x+4）[（4k2+3）x+16k2-12）]=0，由此利用韦达定理、直线垂直，结合题意能求出结果．（3）OM的方程可设为y=kx，与椭圆联立得M点的横坐标为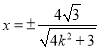，由OM∥l，能求出结果

试题解析：（1）因为左顶点为，所以，又，所以.…………………2分

又因为，

所以椭圆C的标准方程为. ………………………………4分

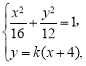（2）直线的方程为，由消元得，.

化简得，，

所以，. ………………………………6分

当时，，

所以.因为点为的中点，所以的坐标为，则.……………………8分

直线的方程为，令，得点坐标为，

假设存在定点，使得，

则，即恒成立，

所以恒成立，所以即

因此定点的坐标为. ……………10分

（3）因为，所以的方程可设为，

由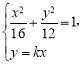得点的横坐标为，…………………12分

由，得

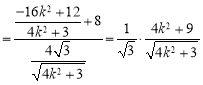…………………14分

，

当且仅当即时取等号，

所以当时，的最小值为． ………………16分