题目内容
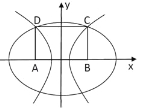
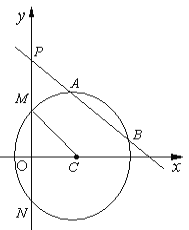
【题目】已知圆心在![]() 轴正半轴上的圆
轴正半轴上的圆![]() 与直线
与直线![]() 相切,与
相切,与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
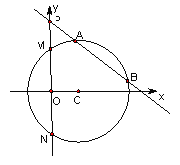
(1)求圆![]() 的标准方程;
的标准方程;
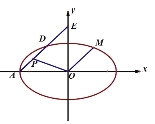
(2)过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若设点
,若设点![]() 为
为![]() 的重心,当
的重心,当![]() 的面积为
的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
试题分析:(1)设圆C的方程为![]() ,利用点C到直线5x+12y+21=0的距离为
,利用点C到直线5x+12y+21=0的距离为![]() ,求出a,即可求圆C的标准方程;(2)利用△MNG的面积为
,求出a,即可求圆C的标准方程;(2)利用△MNG的面积为![]() ,得出|
,得出|![]() |=1,设A
|=1,设A![]() ,B
,B![]() ,则
,则![]() ,即
,即![]() ,直线方程与圆的方程联立,即可得出结论
,直线方程与圆的方程联立,即可得出结论
试题解析:(1)由题意知圆心![]() ,且
,且![]() ,
,
由![]() 知
知![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
于是可设圆![]() 的方程为
的方程为![]() …………2分
…………2分
又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() 或
或![]() (舍),
(舍),
故圆![]() 的方程为
的方程为![]() .…………4分
.…………4分
(2)![]() 的面积
的面积![]() ,所以
,所以![]() .
.
若设![]() ,则
,则![]() ,即
,即![]() ,…………6分
,…………6分
当直线![]() 斜率不存在时,
斜率不存在时,![]() 不存在,
不存在,
故可设直线![]() 为
为![]() ,代入圆
,代入圆![]() 的方程
的方程![]() 中,
中,
可得![]() ,…………8分
,…………8分
则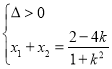 ,即
,即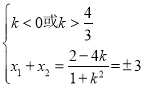 …………10分
…………10分
得![]() 或
或![]() ,
,
故满足条件的直线![]() 的方程为
的方程为![]() 或
或![]() .…………12分
.…………12分

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目