Question

【题目】对某产品1到6月份销售量及其价格进行调查，其售价x和销售量y之间的一组数据如下表所示：

月份i	1	2	3	4	5	6
单价（元）	9	9.5	10	10.5	11	8
销售量（件）	11	10	8	6	5	14

（1）根据1至5月份的数据，求出y关于x的回归直线方程；

（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，则认为所得到的回归直线方程是理想的，试问所得到的回归直线方程是否理想？

（3）预计在今后的销售中，销售量与单价仍然服从（1）中的关系，且该产品的成本是2.5元/件，为获得最大利润，该产品的单价应定为多少元？

Answer 1

【答案】（1）（2）理想；（3）7.5元

【解析】

（1）首先计算，，再根据回归直线公式计算即可.

（2）利用回归直线方程计算时的估计值，再计算误差即可得到结论.

（3）首先求出利润的解析式，再根据二次函数的性质即可得到答案.

（1）由题意知，.

∴，.

∴．

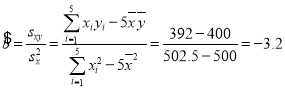（2）由（1）知，当时，，

∴，

∴可认为所得到的回归直线方程是理想的．

（3）依题意得，利润．

∴当元时，L取得最大值．

∴该产品的单价定为7.5元时，利润最大．