题目内容
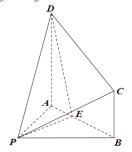
【题目】已知△ABC中,三边长a,b,c满足a2﹣a﹣2b﹣2c=0,a+2b﹣2c+3=0,则这个三角形最大角的大小为_____.
【答案】120°
【解析】
根据条件可得b=![]() ,c=
,c=![]() ,显然c>b,假设c=
,显然c>b,假设c=![]() >a,解得 a<1或a>3,刚好符合,故最大边为c,由余弦定理求得cosC 的值,即可得到C 的值.
>a,解得 a<1或a>3,刚好符合,故最大边为c,由余弦定理求得cosC 的值,即可得到C 的值.
把a2﹣a﹣2b﹣2c=0和a+2b﹣2c+3=0联立可得,b=![]() ,c=
,c=![]() ,显然c>b.
,显然c>b.
比较c与a的大小.
因为b=![]() >0,解得a>3,(a<﹣1的情况很明显为负数舍弃)
>0,解得a>3,(a<﹣1的情况很明显为负数舍弃)
假设c=![]() >a,解得 a<1或a>3,刚好符合,
>a,解得 a<1或a>3,刚好符合,
所以c>a,所以最大边为c.
由余弦定理可得 c2=a2+b2﹣2abcosC,
即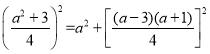 ﹣2a
﹣2a![]() cosC,
cosC,
解得cosC=﹣![]() ,∴C=120°,
,∴C=120°,
故答案为:120°.

练习册系列答案
相关题目
【题目】某企业生产A产品的质量以其质量指标值衡量,质量指标值划分等级及产品售价如下表:
质量指标值m |
|
|
|
产品等级 | 等品 | 二等品 | 三等品 |
售价(每件) | 160元 | 140元 | 120元 |
从该企业生产的A产品中抽取100件作为样本,检测其质量指标值,得到下图的频率分布直方图.
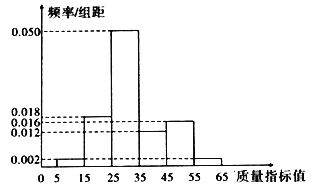
(1)根据频率分布直方图,求A产品质量指标值的中位数;
(2)用样本频率估计总体概率.现有一名顾客随机购买两件A产品,设其支付的费用为X元,求X的分布列及数学期望.