题目内容
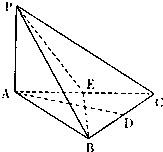 如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为等边三角形,D,E分别是BC,CA的中点.
如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为等边三角形,D,E分别是BC,CA的中点.(1)证明:平面PBE⊥平面PAC;
(2)如何在BC上找一点F,使AD∥平面PEF并说明理由;
(3)若PA=AB=2,对于(Ⅱ)中的点F,求三棱锥P-BEF的体积.
分析:(1)证明平面PBE内的直线BE,垂直平面PAC内的两条相交直线PA、CA,即可证明平面PBE⊥平面PAC;
(2)取CD的中点F,连接EF,证明AD平行平面PEF内的直线EF,即可证明结论;
(3)PA=AB=2,利用VP-BEF=
PA•S△BEF求三棱锥P-BEF的体积.
(2)取CD的中点F,连接EF,证明AD平行平面PEF内的直线EF,即可证明结论;
(3)PA=AB=2,利用VP-BEF=
| 1 |
| 3 |
解答: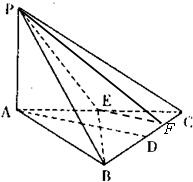 (Ⅰ)证明:∵PA⊥底面ABC,BE?底面ABC,
(Ⅰ)证明:∵PA⊥底面ABC,BE?底面ABC,
∴PA⊥BE.(1分)
又∵△ABC是正三角形,且E为AC的中点,
∴BE⊥CA.(2分)
又PA∩CA=A,
∴BE⊥平面PAC.(4分)
∵BE?平面PBE,
∴平面PBE⊥平面PAC.(6分)
(Ⅱ)解:取CD的中点F,连接EF,则F即为所求.(7分)
∵E,F分别为CA,CD的中点,
∴EF∥AD.(8分)
又EF?平面PEF,AD?平面PEF,
∴AD∥平面PEF.(10分)
(Ⅲ)解,根据题意可得
VP-BEF=
PA•S△BEF=
•2•
•
•
=
.(14分)
 (Ⅰ)证明:∵PA⊥底面ABC,BE?底面ABC,
(Ⅰ)证明:∵PA⊥底面ABC,BE?底面ABC,∴PA⊥BE.(1分)
又∵△ABC是正三角形,且E为AC的中点,
∴BE⊥CA.(2分)
又PA∩CA=A,
∴BE⊥平面PAC.(4分)
∵BE?平面PBE,
∴平面PBE⊥平面PAC.(6分)
(Ⅱ)解:取CD的中点F,连接EF,则F即为所求.(7分)
∵E,F分别为CA,CD的中点,
∴EF∥AD.(8分)
又EF?平面PEF,AD?平面PEF,
∴AD∥平面PEF.(10分)
(Ⅲ)解,根据题意可得
VP-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题考查平面与平面垂直的判定,直线与平面平行的判定,棱锥的体积,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中,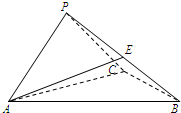 (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2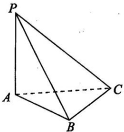 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为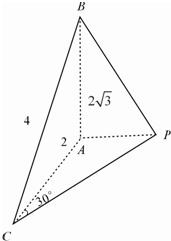 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,