Question

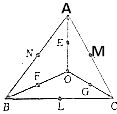
【题目】平面内有一个△ABC和一点O（如图），线段OA，OB，OC的中点分别为E，F，G，BC，CA，AB的中点分别为L，M，N，设 = ， = ， = ．

（1）试用 ， ， 表示向量 ， ， ；
（2）证明：线段EL，FM，GN交于一点且互相平分．

Answer 1

【答案】
（1）解： =；

同理， ，

（2）证明：如图，连接EN，NL，LG，GE，根据条件，则：

NE∥BO，且 ，LG∥BO，且 ；

∴NE∥LG，且NE=LG；

∴四边形NLGE为平行四边形；

∴线段El，GN交于一点且互相平分；

同理，线段EL，FM交于一点且互相平分；

∴线段EL，FM，GN交于一点且互相平分．

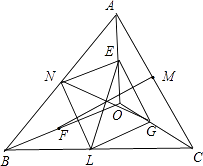
【解析】（1）根据向量的加法、数乘的几何意义，以及向量加法的平行四边形法则，并进行向量的数乘运算便可得到 ，从而同理可以用 分别表示出 ；（2）可连接EN，NL，LG，GE，根据三角形中位线的性质及平行四边形的定义便可得到四边形NLGE为平行四边形，从而对角线EL，GN交于一点且互相平分，而同理可证明EL，FM相交于一点且互相平分，从而便得出线段EL，FM，GN交于一点且互相平分．
【考点精析】解答此题的关键在于理解向量的三角形法则的相关知识，掌握三角形加法法则的特点：首尾相连;三角形减法法则的特点：共起点，连终点，方向指向被减向量．